已知以
为首项的数列
满足:
(1)当
,
,
时,求数列
的通项公式;
(2)当
,
,
时,试用
表示数列
的前
项的和
;
(3)当
(
是正整数),
,
时,求证:数列
,
,
,
成等比数列当且仅当
.
已知A={x|x2-3x+2≤0},B={x|x2-(a+1)x+a≤0}.
(1)若A⊆B,求a的取值范围;
(2)若B⊆A,求a的取值范围.
(本小题满分12分)如图所示,在多面体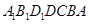 ,四边形
,四边形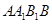 ,
,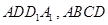 均为正方形,
均为正方形,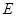 为
为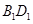 的中点,过
的中点,过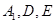 的平面交
的平面交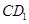 于
于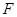

(1)证明: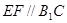 ;
;
(2)(理科做) 求二面角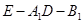 余弦值.
余弦值.
(3)(文科做) 若正方形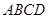 边长为2,求多面体
边长为2,求多面体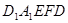 的体积.
的体积.
(本小题满分12分)如图,在正四棱台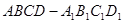 中,
中,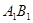 =1,
=1,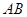 =2,
=2,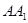 =
=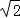 ,
,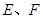 分别是
分别是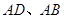 的中点.
的中点.
(1)求证:平面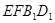 ∥平面
∥平面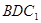 ;
;
(2)求证:平面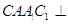 平面
平面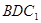 ;
;
(3)(文科不做)求直线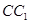 与平面
与平面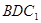 所成的角.
所成的角.
(本小题满分10分)如图,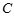 、
、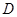 是以
是以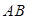 为直径的圆上两点,
为直径的圆上两点, ,
,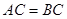 ,
,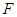 是
是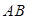 上一点,且
上一点,且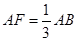 ,将圆沿直径
,将圆沿直径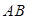 折起,使点
折起,使点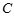 在平面
在平面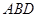 的射影
的射影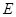 在
在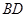 上,已知
上,已知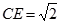 .
.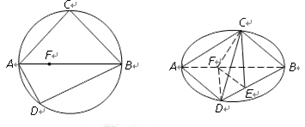
(1)求证: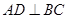 ;
;
(2)求三棱锥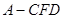 的体积.
的体积.
(本小题满分10分)如图,四棱锥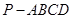 中,
中,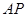 ⊥平面
⊥平面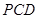 ,
,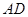 ∥
∥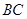 ,
,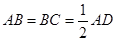 ,
,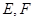 分别为线段
分别为线段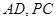 的中点.
的中点.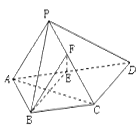
(1)求证: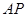
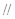 平面
平面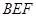 ;
;
(2)求证: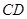 ⊥平面
⊥平面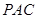 .
.