(本小题满分12分)如图所示,在多面体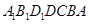 ,四边形
,四边形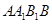 ,
,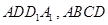 均为正方形,
均为正方形, 为
为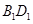 的中点,过
的中点,过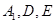 的平面交
的平面交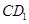 于
于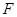

(1)证明: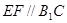 ;
;
(2)(理科做) 求二面角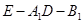 余弦值.
余弦值.
(3)(文科做) 若正方形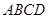 边长为2,求多面体
边长为2,求多面体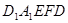 的体积.
的体积.
如图,在正方体ABCD-A1B1C1D1中,对角线A1C与平面BDC1交于点O,AC、BD交于点M,E为AB的中点,F为AA1的中点.求证: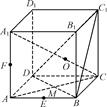
(1)C1、O、M三点共线;
(2)E、C、D1、F四点共面.
如图,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥= AD,BE∥=
AD,BE∥=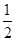 FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.
(1)证明:四边形BCHG是平行四边形.
(2)C、D、F、E四点是否共面?为什么?
在长方体ABCDA1B1C1D1的A1C1面上有一点P(如图所示,其中P点不在对角线B1D1)上.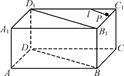
(1)过P点在空间作一直线l,使l∥直线BD,应该如何作图?并说明理由;
(2)过P点在平面A1C1内作一直线m,使m与直线BD成α角,其中α∈ ,这样的直线有几条,应该如何作图?
,这样的直线有几条,应该如何作图?
画一个正方体ABCDA1B1C1D1,再画出平面ACD1与平面BDC1的交线,并且说明理由.
已知椭圆C: +
+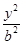 =1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.
=1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.
(1)求椭圆C的标准方程及离心率;
(2)O为坐标原点,P是直线F1A上的一个动点,求|PF2|+|PO|的最小值,并求出此时点P的坐标.