袋中有20个大小相同的球,其中记上0号的有10个,记上
号的有
个(
=1,2,3,4)。现从袋中任取一球.
表示所取球的标号.
(Ⅰ)求
的分布列,期望和方差;
(Ⅱ)若
,试求
的值。
已知函数 的图象在点
的图象在点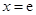 (
(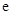 为自然对数的底数)处的切线斜率为3.
为自然对数的底数)处的切线斜率为3.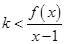 (Ⅰ)求实数
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若 ,且对任意
,且对任意 恒成立,求
恒成立,求 的最大值;
的最大值;
(Ⅲ)当 时,证明
时,证明 .
.
已知椭圆 的离心率为e=
的离心率为e= ,且过点(
,且过点( )
)
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线 :
:
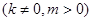 与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(
与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为( ,
, ),求:△OPQ面积的最大值及此时直线
),求:△OPQ面积的最大值及此时直线 的方程.
的方程.
某单位在2012春节联欢会上举行一个抽奖活动:甲箱中装有3个红球,2个黑球,乙箱中装有2个红球4个黑球,参加活动者从这两个箱子中分别摸出1个球,如果摸到的都是红球则获奖.
(Ⅰ)求每个活动参加者获奖的概率;
(Ⅱ)某办公室共有5人,每人抽奖1次,求这5人中至少有3人获奖的概率.
如图,正三棱柱ABC—A1B1C1的底面边长为a,点M在边 BC上,△AMC1是以点M为直角顶点的等腰直角三角形。
(Ⅰ)求证点M为边BC的中点;
(Ⅱ)求点C到平面AMC1的距离;
(Ⅲ)求二面角M—AC1—C的大小。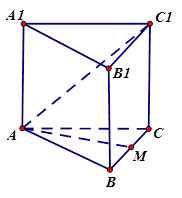
已知函数
(I)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(II)设△ 的内角
的内角 对边分别为
对边分别为 ,且
,且 ,若
,若 与
与 共线,求
共线,求 的值.
的值.