已知数列
和
满足:
其中
为实数,
为正整数。
(Ⅰ)对任意实数
,证明数列
不是等比数列;
(Ⅱ)试判断数列
是否为等比数列,并证明你的结论;
(Ⅲ)设
,
为数列
的前
项和。是否存在实数
,使得对任意正整数
,都有
?若存在,求
的取值范围;若不存在,说明理由。
(12分)已知各项均为正数的数列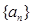 的前n项和为
的前n项和为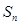 ,且
,且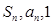 成等差数列.
成等差数列.
(1)求数列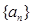 的通项公式;
的通项公式;
(2)若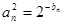 ,设
,设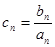 求数列
求数列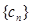 的前项和
的前项和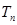 .
.
设函数 ,其中向量
,其中向量 ,
,
(1)求 的最小正周期与单调减区间;
的最小正周期与单调减区间;
(2)在△ABC中, 分别是角A、B、C的对边,已知
分别是角A、B、C的对边,已知 ,△ABC的面积为
,△ABC的面积为 ,求
,求 的值。
的值。
已知一动圆与圆 外切,同时与圆
外切,同时与圆 内切.
内切.
(1)求动圆圆心 的轨迹方程,并说明它是什么样的曲线;
的轨迹方程,并说明它是什么样的曲线;
(2)直线 与M的轨迹相交于不同的两点
与M的轨迹相交于不同的两点 、
、 ,求
,求 的中点的坐标;
的中点的坐标;
(3)求(2)中△OPQ的面积(O为坐标原点).
已知双曲线的中心在坐标原点,焦点在x轴上,渐近线方程为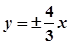 ,且经过点
,且经过点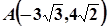 ,设
,设 是双曲线的两个焦点,点
是双曲线的两个焦点,点 在双曲线上,且
在双曲线上,且 =64.
=64.
(1)求双曲线的方程;
(2)求 .
.
已知抛物线以坐标轴为对称轴,原点为顶点,开口向上,且过圆 的圆心.
的圆心.
(1)求此抛物线的方程;
(2)在(1)中所求抛物线上找一点,使这点到直线 的距离最短,并求距离的最小值.
的距离最短,并求距离的最小值.