如图,我市拟在长为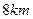 的道路
的道路 的一侧修建一条运动赛道。赛道的前一部分为曲线段
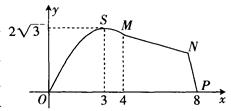
的一侧修建一条运动赛道。赛道的前一部分为曲线段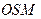 ,该曲线段为函数
,该曲线段为函数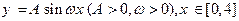 的图像,且图像的最高点为
的图像,且图像的最高点为 ;赛道的后一部分为折线段
;赛道的后一部分为折线段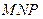 ,为保证参赛运动员的安全,限定
,为保证参赛运动员的安全,限定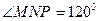 。
。
(1)求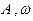 的值和
的值和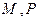 两点间的距离
两点间的距离
(2)应如何设计,才能使折线段赛道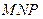 最长
最长
下图为一个平面图形的直观图,请画出它的实际形状. 
图1
下表给出甲、乙、丙三种食物的维生素A、B的含量及成本,营养师想购这三种食物共10千克,使之所含维生素A不少于4 400单位,维生素B不少于4 800单位.
| 甲 |
乙 |
丙 |
|
| 维生素A(单位/千克) |
400 |
600 |
400 |
| 维生素B(单位/千克) |
800 |
200 |
400 |
| 成本(元/千克) |
7 |
6 |
5 |
(1)试用所购甲、乙两种食物的量表示成本;
(2)三种食物各购多少时,成本最低?最低成本是多少?
已知实系数方程x2+ax+2b=0的两根在(0,1)与(1,2)内,求 的取值范围.
的取值范围.
如下图所示,求△PQR内任一点(x,y)满足的关系式.
求z=3x+5y的最大值和最小值,使式中的x、y满足约束条件