某射击测试规则为:每人最多射击3次,击中目标即终止射击,第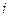 次击中目标得
分,3次均未击中目标得0分.已知某射手每次击中目标的概率为0.8,其各次射击结果互不影响.
次击中目标得
分,3次均未击中目标得0分.已知某射手每次击中目标的概率为0.8,其各次射击结果互不影响.
(Ⅰ)求该射手恰好射击两次的概率;
(Ⅱ)该射手的得分记为
,求随机变量
的分布列及数学期望.
(本小题满分14分)已知函数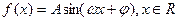 (其中A>0,
(其中A>0, )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为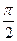 ,且图象上一个最低点为
,且图象上一个最低点为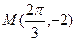 .(Ⅰ)求
.(Ⅰ)求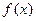 的解析式;(Ⅱ)当
的解析式;(Ⅱ)当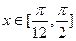 ,求
,求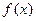 的值域;
的值域;
(本小题满分16分)已知集合M是满足下列性质的函数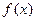 的全体:若存在非零常数k,对任意
的全体:若存在非零常数k,对任意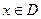 ,等式
,等式 恒成立。(Ⅰ)判断一次函数
恒成立。(Ⅰ)判断一次函数 是否属于集合M;(Ⅱ)证明
是否属于集合M;(Ⅱ)证明 属于集合M,并找到一个常数k;(Ⅲ)已知函数
属于集合M,并找到一个常数k;(Ⅲ)已知函数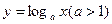 与
与 的图像有公共点,试证明
的图像有公共点,试证明
(本小题满分16分)已知函数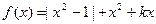 (Ⅰ)若
(Ⅰ)若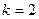 ,求方程
,求方程 的解(Ⅱ)若关于x的方程
的解(Ⅱ)若关于x的方程 在(0,2)上有两个解
在(0,2)上有两个解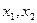 ,求k的取值范围。
,求k的取值范围。
(本小题满分16分)已知数列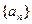 的前n项和为Sn,点
的前n项和为Sn,点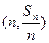 的直线
的直线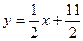 上,数列
上,数列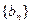 满足
满足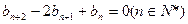 ,
,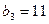 ,且
,且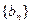 的前9项和为153.
的前9项和为153.
(Ⅰ)求数列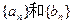 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设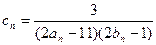 ,记数列
,记数列 的前n项和为Tn,求使不等式
的前n项和为Tn,求使不等式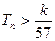 对一切
对一切 都成立的最大正整数k的值.
都成立的最大正整数k的值.
(本小题满分14分)设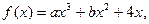 其导函数
其导函数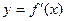 的图象经过点
的图象经过点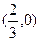 ,(2,0),如右图所示。
,(2,0),如右图所示。
(Ⅰ)求函数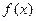 的解析式和极值;
的解析式和极值;
(Ⅱ)对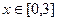 都有
都有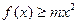 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。