已知函数
,其中
.
(Ⅰ)若曲线
在点
处的切线方程为
,求函数
的解析式;
(Ⅱ)讨论函数
的单调性;
(Ⅲ)若对于任意的
,不等式
在
上恒成立,求
的取值范围.
(本小题满分16分)已知函数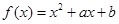 ,
,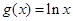 .
.
(1)记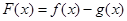 ,求
,求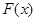 在
在 的最大值;
的最大值;
(2)记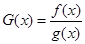 ,令
,令 ,
, ,当
,当 时,若函数
时,若函数 的3个极值点为
的3个极值点为 ,
,
(ⅰ)求证: ;
;
(ⅱ)讨论函数 的单调区间(用
的单调区间(用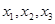 表示单调区间).
表示单调区间).
(本小题满分16分)已知数列 、
、 满足
满足 ,
, ,其中
,其中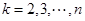 ,则称
,则称 为
为 的“生成数列”.
的“生成数列”.
(1)若数列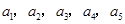 的“生成数列”是
的“生成数列”是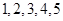 ,求
,求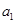 ;
;
(2)若 为偶数,且
为偶数,且 的“生成数列”是
的“生成数列”是 ,证明:
,证明: 的“生成数列”是
的“生成数列”是 ;
;
(3)若 为奇数,且
为奇数,且 的“生成数列”是
的“生成数列”是 ,
, 的“生成数列”是
的“生成数列”是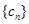 , ,依次将数列
, ,依次将数列 ,
, ,
,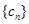 , 的第
, 的第 项取出,构成数列
项取出,构成数列 .探究:数列
.探究:数列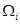 是否为等比数列,并说明理由.
是否为等比数列,并说明理由.
(本小题满分16分)在距A城市45千米的B地发现金属矿,过A有一直线铁路AD.欲运物资于A,B之间,拟在铁路线AD间的某一点C处筑一公路到B.现测得 千米,
千米, (如图).已知公路运费是铁路运费的2倍,设铁路运费为每千米1个单位,总运费为
(如图).已知公路运费是铁路运费的2倍,设铁路运费为每千米1个单位,总运费为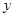 .为了求总运费
.为了求总运费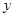 的最小值,现提供两种方案:方案一:设
的最小值,现提供两种方案:方案一:设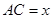 千米;方案二设
千米;方案二设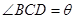 .
.
(1)试将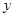 分别表示为
分别表示为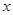 、
、 的函数关系式
的函数关系式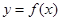 、
、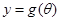 ;
;
(2)请选择一种方案,求出总运费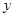 的最小值,并指出C点的位置.
的最小值,并指出C点的位置.
(本小题满分14分)如图,椭圆 和圆
和圆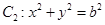 ,已知椭圆
,已知椭圆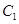 过点
过点 ,焦距为2.
,焦距为2.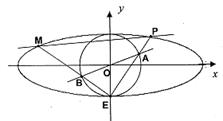
(1)求椭圆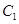 的方程;
的方程;
(2)椭圆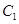 的下顶点为
的下顶点为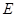 ,过坐标原点
,过坐标原点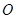 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线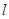 与圆
与圆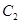 相交于点
相交于点 ,直线
,直线 与椭圆
与椭圆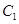 的另一个交点分别是点
的另一个交点分别是点 .设
.设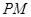 的斜率为
的斜率为 ,直线
,直线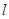 斜率为
斜率为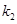 ,求
,求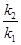 的值.
的值.
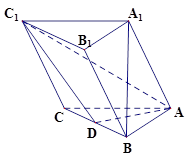
(本小题满分14分)如图,在三棱柱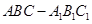 中,
中, 为棱
为棱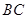 的中点,
的中点,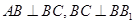 ,
,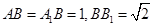 .
.
求证:(1) 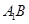
 平面
平面 ;
;
(2)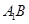 ∥平面
∥平面 .
.