(本小题满分16分)已知数列 、
、 满足
满足 ,
, ,其中
,其中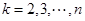 ,则称
,则称 为
为 的“生成数列”.
的“生成数列”.
(1)若数列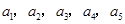 的“生成数列”是
的“生成数列”是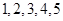 ,求
,求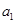 ;
;
(2)若 为偶数,且
为偶数,且 的“生成数列”是
的“生成数列”是 ,证明:
,证明: 的“生成数列”是
的“生成数列”是 ;
;
(3)若 为奇数,且
为奇数,且 的“生成数列”是
的“生成数列”是 ,
, 的“生成数列”是
的“生成数列”是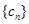 , ,依次将数列
, ,依次将数列 ,
, ,
,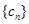 , 的第
, 的第 项取出,构成数列
项取出,构成数列 .探究:数列
.探究:数列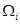 是否为等比数列,并说明理由.
是否为等比数列,并说明理由.
(本小题满分12分)已知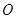 为坐标原点,向量
为坐标原点,向量 ,
, ,
, 点
点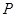 是直线
是直线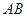 上一点,且
上一点,且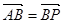 ;
;
(1)设函数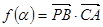 ,
,  ,讨论
,讨论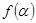 的单调性,并求其值域;
的单调性,并求其值域;
(2)若点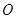 、
、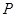 、
、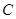 共线,求
共线,求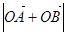 的值。
的值。
(本小题满分12分)某班从6名班干部中(男生4人,女生2人)选3人参加学校义务劳动;(1)求男生甲或女生乙被选中的概率;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率;
(3)设所选3人中女生人数为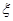 ,求
,求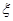 的分布列及数学期望。
的分布列及数学期望。
在直角坐标系xOy中,以O为圆心的圆与直线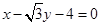 相切。
相切。
(1)求圆O的方程。
(2)圆O与x轴相交于A、B两点,圆O内的动点P使|PA|,|PO|,|PB|成等比数列,求 ·
· 的取值范围.
的取值范围.
已知向量m=(cos ,1),n=(
,1),n=(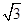 sin
sin ,cos2
,cos2 ).
).
(1)若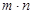 =1,求
=1,求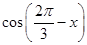 的值;
的值;
(2)记f(x)=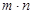 ,在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
复数z1=3+4i,z2=0,z3=c+(2c-6)i在复平面内对应的点分别为A、B、C,若∠BAC是钝角,求实数c的取值范围.