某班数学兴趣小组有男生和女生各3名,现从中任选2名学生去参加校数学竞赛,求
(I) 恰有一名参赛学生是男生的概率;
(II)至少有一名参赛学生是男生的概率;
(Ⅲ)至多有一名参赛学生是男生的概率。
(本小题满分12分)已知向量 =(
=(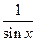 ,
,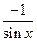 ),
),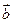 =(2,cos2x).
=(2,cos2x).
(1)若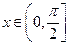 ,试判断
,试判断 与
与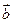 能否平行?
能否平行?
(2)若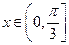 ,求函数f(x)=
,求函数f(x)=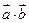 的最小值.
的最小值.
.已知函数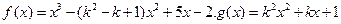 ,其中
,其中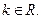
(1)设函数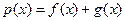 ,若
,若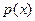 在区间
在区间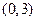 上不是单调函数,求
上不是单调函数,求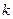 的取值范围.
的取值范围.
(2)设函数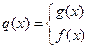
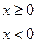 是否存在
是否存在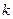 ,对任意给定的非零实数
,对任意给定的非零实数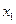 ,存在唯一的非零
,存在唯一的非零
实数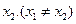 使得
使得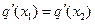 成立,若存在,求
成立,若存在,求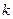 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知中心在原点的双曲线C的右焦点为(2,0),实轴长为2.
(1)求双曲线C的方程;
(2)若直线l:y=kx+与双曲线C左支交于A、B两点,求k的取值范围;
(3)在(2)的条件下,线段AB的垂直平分线l0与y轴交于M(0,m),求m的取值范围.
若函数f(x)=ax3 -bx+4,当x=2时,函数f(x)有极值-.
-bx+4,当x=2时,函数f(x)有极值-.
(1)求函数的解析式;
(2)若关于x的方程f(x)=k有三个根,求实数k的取值范围
已知过抛物线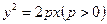 的焦点,斜率为
的焦点,斜率为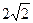 的直线交抛物线于
的直线交抛物线于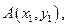
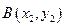 (
(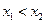 )两点,且
)两点,且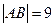 .
.
(1)求该抛物线的方程;
(2)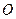 为坐标原点,
为坐标原点,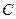 为抛物线上一点,若
为抛物线上一点,若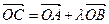 ,求
,求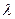 的值
的值