某种项目的射击比赛,开始时在距目标100m处射击,如果命中记3分,且停止射击;若第一次射击未命中,可以进行第二次射击,但目标已在150m处,这时命中记2分,且停止射击;若第二次仍未命中,还可以进行第三次射击,此时目标已在200m处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分,且比赛结束.已知射手甲在100m处击中目标的概率为 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
(1)求射手甲在这次射击比赛中命中目标的概率;
(2)求射手甲在这次射击比赛中得分的数学期望.
已知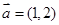 ,
,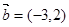 ,当
,当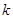 为何值时,
为何值时,
(1) 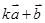 与
与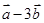 垂直?(2)
垂直?(2) 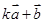 与
与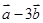 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
已知圆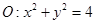 和圆
和圆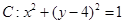 .
.
(1)判断圆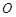 和圆
和圆 的位置关系;
的位置关系;
(2)过圆 的圆心
的圆心 作圆
作圆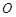 的切线
的切线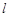 ,求切线
,求切线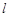 的方程;
的方程;
(3)过圆 的圆心
的圆心 作动直线
作动直线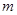 交圆
交圆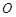 于A,B两点.试问:在以AB为直径的所有圆中,是否存在这样的圆
于A,B两点.试问:在以AB为直径的所有圆中,是否存在这样的圆 ,使得圆
,使得圆 经过点
经过点 ?若存在,求出圆
?若存在,求出圆 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
设数列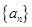 的前
的前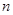 项和
项和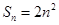 ,
,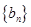 为等比数列,且
为等比数列,且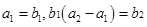 .
.
(1)求数列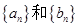 的通项公式;(2)设
的通项公式;(2)设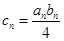 ,求数列
,求数列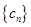 前
前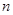 项和
项和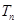 .
.
如图,在正方体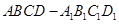 中,
中,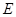 是
是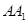 的中点.
的中点.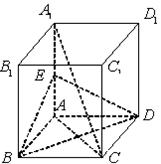
(1)求证: 平面
平面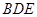 ;
;
(2)求证:平面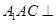 平面
平面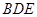 ;
;
(3)求直线BE与平面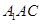 所成角的正弦值.
所成角的正弦值.
在△ABC中,角A,B,C所对边长分别为a,b,c,且c=3,C=60°
(1)若a=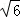 ,求角A;(2)若
,求角A;(2)若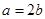 ,求△ABC的面积.
,求△ABC的面积.