已知圆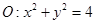 和圆
和圆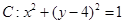 .
.
(1)判断圆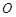 和圆
和圆 的位置关系;
的位置关系;
(2)过圆 的圆心
的圆心 作圆
作圆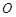 的切线
的切线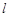 ,求切线
,求切线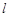 的方程;
的方程;
(3)过圆 的圆心
的圆心 作动直线
作动直线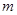 交圆
交圆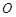 于A,B两点.试问:在以AB为直径的所有圆中,是否存在这样的圆
于A,B两点.试问:在以AB为直径的所有圆中,是否存在这样的圆 ,使得圆
,使得圆 经过点
经过点 ?若存在,求出圆
?若存在,求出圆 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
已知函数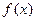 =
=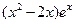 (e为自然对数的底数)
(e为自然对数的底数)
(Ⅰ)求函数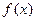 单调递增区间;
单调递增区间;
(Ⅱ)若 ,求函数
,求函数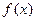 在区间[0,
在区间[0,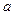 ]上的最大值和最小值.
]上的最大值和最小值.
(III)若函数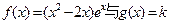 的图象有三个不同的交点,求实数k的取值范围.
的图象有三个不同的交点,求实数k的取值范围.
(参考数据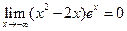 )
)
已知动点P与双曲线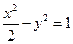 的两个焦点F1,F2的距离之和为定值,
的两个焦点F1,F2的距离之和为定值,
且cos∠F1PF2的最小值为-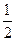 .
.
(1)求动点P的轨迹方程;
(2)是否存在直线l与P点轨迹交于不同的两点M、N,且线段MN恰被直线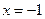 平分?若存在,求出直线l的斜率k的取值范围,若不存在说明理由.
平分?若存在,求出直线l的斜率k的取值范围,若不存在说明理由.
如图,已知正方体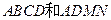 边长都为2,且
边长都为2,且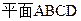
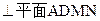 ,
,
E是BC的中点,F是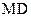 的中点,
的中点,
(1)求证: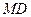
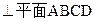 。
。
(2)求点A到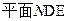 的距离。
的距离。
(3)求证:CF∥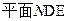 。
。
(4) 求二面角E-ND-A的平面角大小的
余弦值。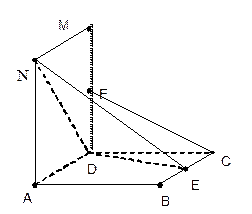
一蒸汽机火车每小时消耗煤的费用与火车行驶的速度的立方成正比,已知速度为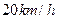 时,每小时消耗的煤价值40元,其余费用每小时1250元,问火车行驶的速度是多少时(速度不超过
时,每小时消耗的煤价值40元,其余费用每小时1250元,问火车行驶的速度是多少时(速度不超过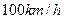 ),全程
),全程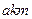 费用最少?
费用最少?
已知函数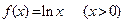 ,函数
,函数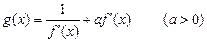
⑴函数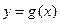 在
在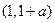 处的切线与
处的切线与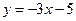 平行 ,求
平行 ,求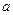 的值;
的值;
⑵在⑴的条件下,求直线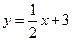 与函数
与函数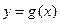 的图象所围成图形的面积.
的图象所围成图形的面积.