已知函数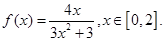
(Ⅰ)求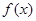 的值域;
的值域;
(Ⅱ)设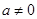 ,函数
,函数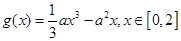 .若对任意
.若对任意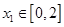 ,总存在
,总存在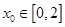 ,使
,使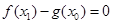 ,求实数
,求实数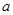 的取值范围.
的取值范围.
(本小题10分)
已知等差数列{an}中,a3 + a4 = 15,a2a5 = 54,公差d < 0.
(1)求数列{an}的通项公式an ;
;
(2)求数列的前n项和Sn的最大值及相应的n的值.
(本小题10分)
在△ABC中, ,求
,求 .
.
.
已知关于x的方程2x2-(+1)x+m=0的两根为sinθ和cosθ,θ∈(0,2π),求:(1) 的值;
的值;
(2)m的值;
(3)方程的两根及此时θ的值.
.
设平面内的向量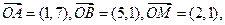 点
点 是直线
是直线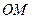 上的一个动点,求当
上的一个动点,求当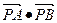 取最小值时,
取最小值时,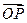 的坐标及
的坐标及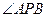 的余弦值。
的余弦值。
.
设y="A" sin(ωx+j)(A>0,ω>0,|j|<π)最高点D的坐标为(2,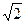 ),由
),由 最高点运动到相邻的最低点时,曲线与
最高点运动到相邻的最低点时,曲线与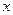 轴交点E的坐标为(6,0),(1)求A、ω、j的值;(2)求出该函数的频率,初相和单调区间.
轴交点E的坐标为(6,0),(1)求A、ω、j的值;(2)求出该函数的频率,初相和单调区间.