(本小题满分12分)已知函数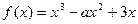
(1)若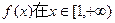 上增函数,求实数a的取值范围;
上增函数,求实数a的取值范围;
(2)若x=3是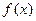 的极值点,求
的极值点,求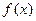 在
在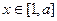 上的最小值和最大值.
上的最小值和最大值.
已知A={a+2,(a+1)2,a2+3a+3}且1∈A,求实数a的值.
已知集合A={x|(x-2)[x-(3a+1)]<0},B=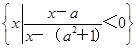 .
.
(1) 当a=2时,求A∩B;
(2) 求使B真包含于A的实数a的取值范围.
已知集合A={y|y=-2x,x∈[2,3]},B={x|x2+3x-a2-3a>0}.若A B,求实数a的取值范围.
B,求实数a的取值范围.
集合A={x|-2≤x≤5},集合B={x|m+1≤x≤2m-1}.
(1)若B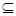 A,求实数m的取值范围;
A,求实数m的取值范围;
(2)当x∈R时,没有元素x使x∈A与x∈B同时成立,求实数m的取值范围.
集合A= ,集合B={a2,a+b,0},若A=B,求a2 013+b2 014的值.
,集合B={a2,a+b,0},若A=B,求a2 013+b2 014的值.