某学校拟建一座长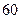 米,宽
米,宽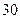 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔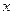 米需打建一个桩位,每个桩位需花费
米需打建一个桩位,每个桩位需花费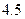 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的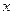 米墙面需花
米墙面需花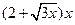 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当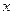 为何值时,所需总费用最少?
为何值时,所需总费用最少?
证明以下命题:
(1)对任一正整数
,都存在正整数
,使得
成等差数列;
(2)存在无穷多个互不相似的三角形
,其边长
为正整数且
成等差数列.
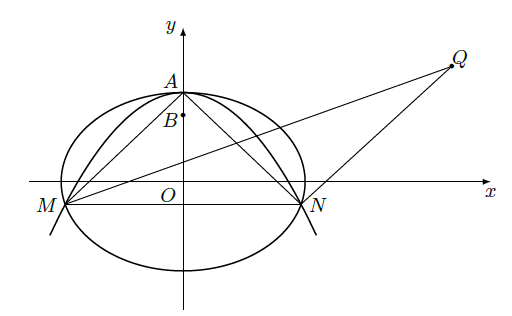
设椭圆 : ,抛物线 : .
(1) 若
经过
的两个焦点,求
的离心率;
(2) 设
,又
为
与
不在
轴上的两个交点,若
的垂心为
,且
的重心在
上,求椭圆
和抛物线
的方程.
如图,
与
都是边长为2的正三角形,
平面
平面
,
平面
,
.
(1)求点
到平面
的距离;
(2)求平面
与平面
所成二面角的正弦值.
设函数
.
(1)当
时,求
的单调区间;
(2)若
在
上的最大值为
,求
的值.
某迷宫有三个通道,进入迷宫的每个人都要经过一个智能门,首次到达此门,系统会随机(即等可能)为你打开一个通道.若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门.再次到达智能门时,系统会随机打开一个你未到过的通道,直至走出迷宫为止.令
表示走出迷宫所需的时间.
(1)求
的分布列;
(2)求
的数学期望.