(本小题满分12分)学校文娱队的每位队员唱
歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中任选2人.设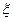 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且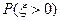 =.
=.
(Ⅰ)求文娱队的人数;
(Ⅱ)写出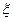 的概率分布列并计算
的概率分布列并计算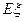 .
.
(本小题满分12分)已知z,y之间的一组数据如下表:
| x |
1 |
3 |
6 |
7 |
8 |
| y |
1 |
2 |
3 |
4 |
5 |
(1)从x ,y中各取一个数,求x+y≥10的概率;
(2)对于表中数据,甲、乙两同学给出的拟合直线分别为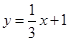 与
与 ,试利用“最小平方法(也称最小二乘法)”判断哪条直线拟合程度更好.
,试利用“最小平方法(也称最小二乘法)”判断哪条直线拟合程度更好.
(本小题满分12分)已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m的值;
(2)若 ,求实数m的取值范围.
,求实数m的取值范围.
给定数列 ,如果存在常数
,如果存在常数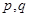 使得
使得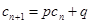 对任意
对任意 都成立,则称
都成立,则称 为“M类数列”
为“M类数列”
(1)若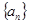 是公差为
是公差为 的等差数列,判断
的等差数列,判断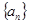 是否为“M类数列”,并说明理由;
是否为“M类数列”,并说明理由;
(1)若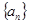 是“M类数列”且满足:
是“M类数列”且满足: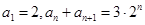
①求 及
及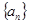 的通项公式;
的通项公式;
②设数列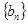 满足:对任意的正整数
满足:对任意的正整数 ,都有
,都有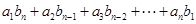
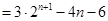 ,且集合
,且集合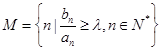 中有且仅有3个元素,试求实数
中有且仅有3个元素,试求实数 的取值范围.
的取值范围.
已知数列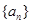 的前n项和是
的前n项和是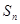 ,且
,且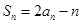
(1)证明: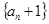 为等比数列;
为等比数列;
(2)证明: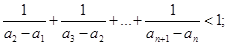
(3)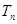 为数列
为数列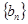 的前n项和,设
的前n项和,设 ,是否存在正整数m,k,使
,是否存在正整数m,k,使 成立,若存在,求出m,k;若不存在,说明理由.
成立,若存在,求出m,k;若不存在,说明理由.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米,设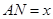 米,花坛AMPN的面积为
米,花坛AMPN的面积为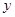 平方米
平方米
(1)求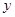 关于
关于 的函数解析式和定义域;
的函数解析式和定义域;
(2)要使花坛AMPN的面积大于32平方米,求 的取值范围;
的取值范围;
(3)当AM,AN的长度分别是多少时,花坛AMPN的面积最小,并求出最小面积.