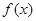 是定义在
是定义在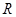 上的偶函数,当
上的偶函数,当 时,
时,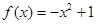 ;当
;当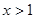 时,
时,
(Ⅰ)当 时,求满足方程
时,求满足方程 的
的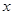 的值
的值
(Ⅱ)求 在
在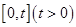 上的值域.
上的值域.
已知函数 ,且f(1)=
,且f(1)=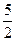 ,f(2)=
,f(2)= .(1)求
.(1)求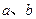 ;(2)判断
;(2)判断 f(x)的奇偶性;(3)试判断函数在
f(x)的奇偶性;(3)试判断函数在 上的单调性,并证明。
上的单调性,并证明。
已知 ,
, ,
,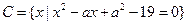 ;若
;若 ,求
,求 的值
的值
(1)化简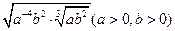
(2)计算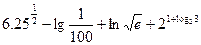 的值
的值
((本题14分)定义:若函数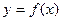 在某一区间D上任取两个实数
在某一区间D上任取两个实数 、
、 ,且
,且 ,都有
,都有 ,则称函数
,则称函数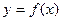 在区间D上具有性质L。
在区间D上具有性质L。
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明)。
(2)对于函数 ,判断其在区间
,判断其在区间 上是否具有性质L?并用所给定义证明你的结论。
上是否具有性质L?并用所给定义证明你的结论。
(3)若函数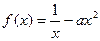 在区间(0,1)上具有性质L,求实数
在区间(0,1)上具有性质L,求实数 的取值范围。
的取值范围。
((本题14分)已知函数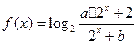 (
(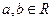 )的图象过点(1,2),它的反函数的图象也过点(1,2)。
)的图象过点(1,2),它的反函数的图象也过点(1,2)。
(1)求实数 的值,并求函数
的值,并求函数 的定义域和值域;
的定义域和值域;
(2)判断函数 在其定义域上的单调性(不必证明),并解不等式
在其定义域上的单调性(不必证明),并解不等式 。
。