已知椭圆 的离心率为
的离心率为 ,长轴长为
,长轴长为 ,直线
,直线 交椭圆于不同的两点A、B。
交椭圆于不同的两点A、B。
(1)求椭圆的方程;
(2)求 的值(O点为坐标原点);
的值(O点为坐标原点);
(3)若坐标原点O到直线 的距离为
的距离为 ,求
,求 面积的最大值。
面积的最大值。
下表是关于宿州市服装机械厂某设备的使用年限 (年)和所需要的维修费用
(年)和所需要的维修费用 (万元)的几组统计数据:
(万元)的几组统计数据:
 |
2 |
3 |
4 |
5 |
6 |
 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
(Ⅰ)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程;
的线性回归方程;
(Ⅱ)估计使用年限为10年时,维修费用为多少?
(参考:(1)
(2) )
)
已知 ,求证:
,求证: .
.
实数 取什么数值时,复数
取什么数值时,复数 分别是:
分别是:
(Ⅰ)实数;(Ⅱ)纯虚数.
设函数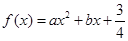 在
在 处取得极值,且曲线
处取得极值,且曲线 在点
在点 处的切线垂直于直线
处的切线垂直于直线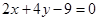 .
.
(Ⅰ) 求 的值;
的值;
(Ⅱ)求曲线 和直线
和直线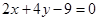 所围成的封闭图形的面积;
所围成的封闭图形的面积;
(Ⅲ)设函数 ,若方程
,若方程 有三个不相等的实根,求
有三个不相等的实根,求 的取值范围.
的取值范围.
已知函数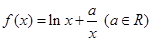
(I)讨论函数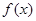 的单调性;
的单调性;
(Ⅱ)当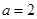 时,求函数
时,求函数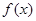 在区间
在区间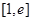 上的最值.
上的最值.