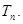(本小题满分12分)已知函数 的最小正周期为
的最小正周期为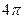 .
.
(1)求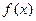 的单调递增区间;
的单调递增区间;
(2)在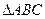 中,角
中,角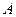 ,
,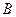 ,
,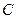 的对边长分别是
的对边长分别是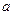 ,
, ,
, 满足
满足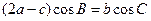 ,求函数
,求函数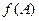 的取值范围.
的取值范围.
已知函数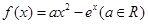
(Ⅰ)当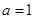 时,判断函数
时,判断函数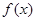 的单调区间并给予证明;
的单调区间并给予证明;
(Ⅱ)若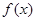 有两个极值点
有两个极值点 ,证明:
,证明: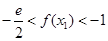 .
.
(本小题满分12分)已知抛物线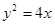 ,直线
,直线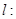
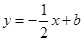 与抛物线交于
与抛物线交于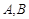 两点.
两点.
(Ⅰ)若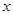 轴与以
轴与以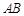 为直径的圆相切,求该圆的方程;
为直径的圆相切,求该圆的方程;
(Ⅱ)若直线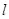 与
与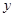 轴负半轴相交,求
轴负半轴相交,求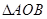 面积的最大值.
面积的最大值.
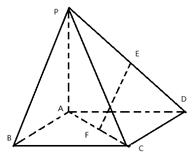
(本小题满分12分)如图所示,在四棱锥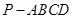 中,底面
中,底面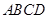 为正方形,侧棱
为正方形,侧棱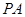
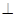 底面
底面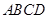 ,
,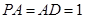 ,
,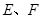 分别为
分别为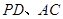 上的动点,且
上的动点,且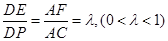 .
.
(Ⅰ)若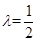 ,求证:
,求证: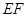 //
//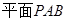
(Ⅱ)求三棱锥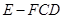 体积最大值.
体积最大值.
(本小题满分12分)随机抽取某中学高三年级甲乙两班各10名同学,测量出他们的身高(单位:cm),获得身高数据的茎叶图如图,其中甲班有一个数据被污损.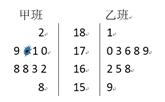
(Ⅰ)若已知甲班同学身高平均数为170cm,求污损处的数据;
(Ⅱ)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高176cm的同学被抽中的概率.
(本小题满分12分)已知数列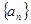 的各项均为正数,前
的各项均为正数,前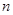 项和为
项和为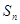 ,且
,且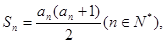
(Ⅰ)求证数列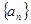 是等差数列;
是等差数列;
(Ⅱ)设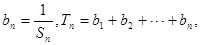 求
求