袋中有大小相同的若干个小球,分别为红色、黑色、黄色、绿色,从中任取一个球,已知得到红球的概率是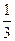 ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是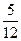 ,得到黄球或绿球的概率也是
,得到黄球或绿球的概率也是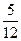 ,试求得到黑球、得到黄球、得到绿球的概率各是多少?
,试求得到黑球、得到黄球、得到绿球的概率各是多少?
已知函数 为常数)是实数集R上的奇函数,函数
为常数)是实数集R上的奇函数,函数 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数.
(1)求a的值; (2)若 上恒成立,求
上恒成立,求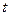 的取值范围;
的取值范围;
(3)讨论关于 的根的个数.
的根的个数.
设函数

 .对于正项数列
.对于正项数列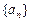 ,其前
,其前
(1)求实数 (2)求数列
(2)求数列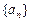 的通项公式
的通项公式
(3)若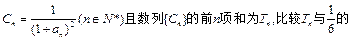 大小,并说明理由。
大小,并说明理由。
设函数 定义域为
定义域为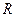 ,当
,当 时,
时, ,且对于任意的
,且对于任意的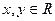 ,都有
,都有
(1)求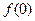 的值,并证明函数
的值,并证明函数 在
在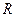 上是减函数;
上是减函数;
(2)记△ABC的三内角A、B、C的对应边分别为a,b,c,若 时,不等式
时,不等式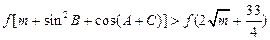 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
)设函数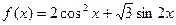 ,
,
(1)求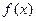 的周期以及单调增区间; (2)若
的周期以及单调增区间; (2)若 ,求sin2x的值;
,求sin2x的值;
(3)在△ABC中,a,b,c分别是角A,B,C的对边,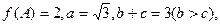 求b,c的长。
求b,c的长。
设函数
(1)求 的单调增区间和单调减区间;
的单调增区间和单调减区间;
(2)若当 时(其中e=2.71828…),不等式
时(其中e=2.71828…),不等式 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)若关于x的方程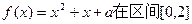 上恰有两个相异的实根,求实数a的取值范围。
上恰有两个相异的实根,求实数a的取值范围。