(本小题满分12分)
班主任为了对本班学生的考试成绩进行分析,决定从全班25位女同学,15位男同学中随机抽取一个容量为8的样本进行分析.
(1)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(2)随机抽取8位同学,数学分 数依次为:60,65,70,75,80,85,90,95;
数依次为:60,65,70,75,80,85,90,95;
物理成绩依次为:72,77,80,84,88,90,93,95,
①若规定90分(含90分)以上为优秀,记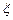 为这8位同学中数学和物理分数均为优秀的人数,求
为这8位同学中数学和物理分数均为优秀的人数,求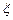 的分布列和数学期望;
的分布列和数学期望;
②若这8位同学的数学、物理分数事实上对应下表:
| 学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
数学分数 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
物理分数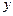 |
72 |
77 |
80 |
84 |
88 |
90 |
93 |
95 |
根据上表数据可知,变量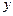 与
与 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出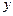 与
与 的线性回归方程(系数精确到0.01).(参考公式:
的线性回归方程(系数精确到0.01).(参考公式: ,其中
,其中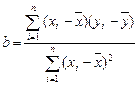 ,
,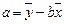 ;参考数据:
;参考数据: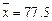 ,
, ,
, ,
,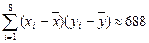 ,
, ,
, ,
,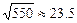 )
)
已知函数 ,
, .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)在锐角三角形 中,若
中,若 ,
, ,求△
,求△ 的面积.
的面积.
如图,正三棱锥 的底面边长为
的底面边长为 ,侧棱长为
,侧棱长为 ,
, 为棱
为棱 的中点.
的中点.
(1)求异面直线 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)求该三棱锥的体积 .
.
设二次函数 ,对任意实数
,对任意实数 ,有
,有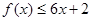 恒成立;数列
恒成立;数列 满足
满足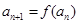 .
.
(1)求函数 的解析式和值域;
的解析式和值域;
(2)证明:当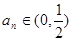 时,数列
时,数列 在该区间上是递增数列;
在该区间上是递增数列;
(3)已知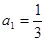 ,是否存在非零整数
,是否存在非零整数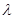 ,使得对任意
,使得对任意 ,都有
,都有
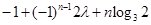 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由.
已知函数 为奇函数.
为奇函数.
(1)求常数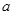 的值;
的值;
(2)判断函数的单调性,并说明理由;
(3)函数 的图象由函数
的图象由函数 的图象先向右平移2个单位,再向上平移2个单位得到,写出
的图象先向右平移2个单位,再向上平移2个单位得到,写出 的一个对称中心,若
的一个对称中心,若 ,求
,求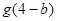 的值.
的值.
上海某化学试剂厂以x千克/小时的速度生产某种产品(生产条件要求 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是 元.
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产运输900千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求最大利润.