(本小题满分12分)
“神州”号飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回舱预 计到达的区域安排了同一条直线上的三个救援中心(记为
计到达的区域安排了同一条直线上的三个救援中心(记为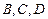 ).当返回舱距地面1万米的
).当返回舱距地面1万米的 点时(假定以后垂直下落,并在
点时(假定以后垂直下落,并在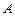 点着陆),
点着陆),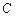 救援中心测得飞船位于其南偏东
救援中心测得飞船位于其南偏东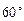 方向,仰角为
方向,仰角为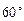 ,
,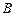 救援中心测得飞船位于其南偏西
救援中心测得飞船位于其南偏西 方向,仰角为
方向,仰角为 .
. 救援中心测得着陆点
救援中心测得着陆点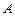 位于其正东方向.
位于其正东方向.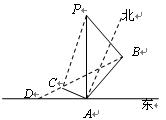
(1)求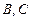
 两救援中心间的距离;
两救援中心间的距离;
(2) 救援中心与着陆点
救援中心与着陆点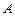 间的距离.
间的距离.
已知圆O: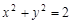 交x轴于A,B两点,曲线C是以AB为长轴,离心率为
交x轴于A,B两点,曲线C是以AB为长轴,离心率为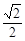 的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交直线
的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交直线 于点Q.
于点Q.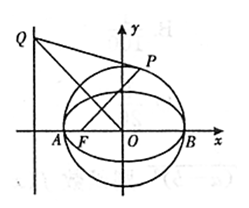
(1)求椭圆C的标准方程;
(2)若点P的坐标为(1,1),求证:直线PQ圆O相切;
(3)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由.
已知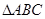 中,
中,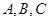 的对边分别为
的对边分别为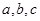 ,且
,且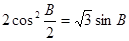 ,
, 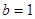
(1)若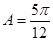 ,求边
,求边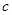 的大小;
的大小;
(2)求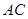 边上高的最大值.
边上高的最大值.
如图,已知多面体 中,
中,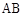
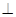 平面
平面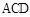 ,
,
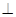 平面
平面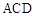 ,
,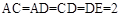 ,
,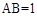 ,
,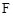 为
为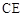 的中点
的中点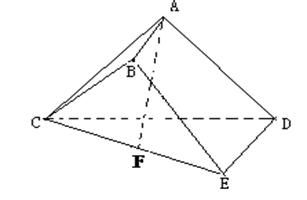
(1)求证: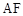
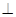
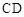 ;
;
(2)求多面体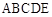 的体积.
的体积.
某高校在2012年的自主招生考试
成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示
(1)求出频率分布表中①、②位置相应的数据;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第
二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行而试,求第4组至少有一名学生被考官A面试的概率?
(Ⅰ)已知函数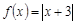 ,
, , 若
, 若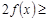
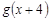 恒成立,求实数
恒成立,求实数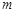 的
的
取值范围.
(Ⅱ)已知实数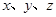 满足
满足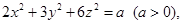 且
且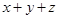 的最大值是1,求
的最大值是1,求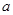 的值.
的值.