二次函数f(x)=ax2+x+1(a>0)的图象与x轴的两个不同的交点的横坐标分别为x1、x2。
(1)证明:(1+x1)(1+x2)=1;
(2)证明:x1<-1,x2<-1;
(3)若函数y=xf(x)在区间(- ,-4)
,-4) 上单调递增,试求a的取值范围。
上单调递增,试求a的取值范围。
某车间加工零件的数量 与加工时间
与加工时间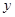 的统计数据如表:
的统计数据如表:
零件数 (个) (个) |
10 |
20 |
30 |
加工时间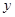 (分钟) (分钟) |
21 |
30 |
39 |
现已求得上表数据的回归方程 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为()
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为()
A.112分钟 B.102分钟 C.94分钟 D.84分钟
已知函数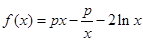 .
.
(1)若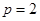 ,求曲线
,求曲线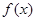 在点
在点 处的切线方程;
处的切线方程;
(2)若函数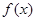 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
(3)设函数 ,若在
,若在 上至少存在一点
上至少存在一点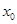 ,使得
,使得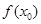 >
> 成立,求实数
成立,求实数 的取值范围.
的取值范围.
请你设计一个包装盒,如图所示, 是边长为
是边长为 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,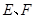 在
在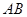 上是被切去的等腰直角三角形斜边的两个端点,设
上是被切去的等腰直角三角形斜边的两个端点,设 .
.
(1)若广告商要求包装盒侧面积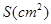 最大,试问
最大,试问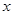 应取何值?
应取何值?
(2)若广告商要求包装盒容积 最大,试问
最大,试问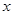 应取何值?并求出此时包装盒的高与底面边长的比值.
应取何值?并求出此时包装盒的高与底面边长的比值.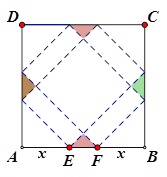
已知 为偶函数,曲线
为偶函数,曲线 过点
过点 ,
,  .
.
(1)若曲线 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围;
的取值范围;
(2)若当 时函数
时函数 取得极值,确定
取得极值,确定 的单调区间.
的单调区间.
用反证法证明:已知 ,
, ,
, ,求证:
,求证: ,
, ,
, .
.