如图,已知抛物线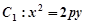 的焦点在抛物线
的焦点在抛物线 上,点
上,点 是抛物线
是抛物线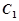 上的动点.
上的动点.
(Ⅰ)求抛物线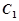 的方程及其准线方程;
的方程及其准线方程;
(Ⅱ)过点 作抛物线
作抛物线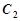 的两条切线,
的两条切线,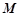 、
、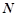 分别为两个切点,设点
分别为两个切点,设点 到直线
到直线 的距离为
的距离为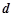 ,求
,求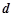 的最小值.
的最小值.
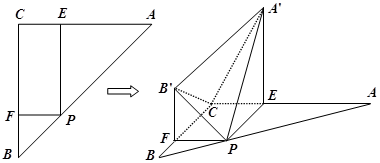
如图,在△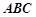 中,
中,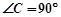 ,
,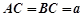 ,点
,点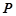 在
在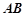 上,
上,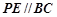 交
交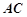 于
于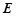 ,
,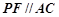 交
交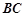 于
于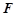 .沿
.沿 将△
将△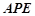 翻折成△
翻折成△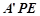 ,使平面
,使平面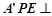 平面
平面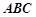 ;沿
;沿 将△
将△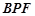 翻折成△
翻折成△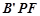 ,使平面
,使平面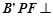 平面
平面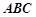 .
.
(Ⅰ)求证: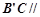 平面
平面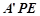 .
.
(Ⅱ)设 ,当
,当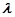 为何值时,二面角
为何值时,二面角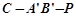 的大小为
的大小为 ?
?
一个袋中装有大小相同的黑球和白球共9个,从中任取3个球,记随机变量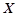 为取出3球中白球的个数,已知
为取出3球中白球的个数,已知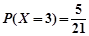 .
.
(Ⅰ)求袋中白球的个数;
(Ⅱ)求随机变量 的分布列及其数学期望.
的分布列及其数学期望.
在△ 中,角
中,角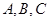 所对的边分别为
所对的边分别为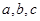 ,满足
,满足 .
.
(Ⅰ)求角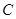 ;
;
(Ⅱ)求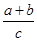 的取值范围.
的取值范围.
已知函数 ,当
,当 时函数
时函数 取得一个极值,其中
取得一个极值,其中 .
.
(Ⅰ)求 与
与 的关系式;
的关系式;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)当 时,函数
时,函数 的图象上任意一点的切线的斜率恒大于
的图象上任意一点的切线的斜率恒大于 ,求
,求 的取值范围.
的取值范围.