6女,4男中随机选出3位参加测验.每位女同学能通过测验的概率为0.8,每位男同学能通过测验的概率为0.6.试求:
⑴选出的3位同学中,至少有一位男同学的概率;
⑵10位同学中的女同学甲和男同学乙同时被先选中且通过测验的概率.
在△ABC中,角A,B,C所对的边分别为a,b,c,已知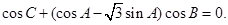
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
已知函数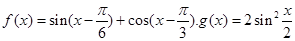 。
。
(1)若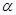 是第一象限角,且
是第一象限角,且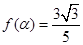 。求
。求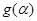 的值;
的值;
(2)求使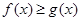 成立的x的取值集合。
成立的x的取值集合。
已知函数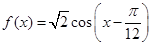 ,
,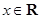 .
.
(1) 求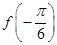 的值;
的值;
(2) 若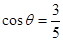 ,
,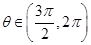 ,求
,求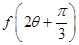 .
.
已知函数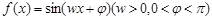 的周期为
的周期为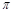 ,图象的一个对称中心为
,图象的一个对称中心为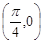 ,将函数
,将函数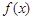 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个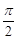 单位长度后得到函数
单位长度后得到函数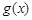 的图象。
的图象。
(1)求函数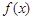 与
与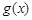 的解析式
的解析式
(2)是否存在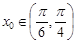 ,使得
,使得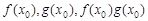 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定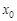 的个数,若不存在,说明理由;
的个数,若不存在,说明理由;
(3)求实数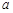 与正整数
与正整数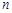 ,使得
,使得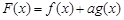 在
在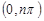 内恰有2013个零点
内恰有2013个零点
设 的内角A、B、C的对边分别为a、b、c,
的内角A、B、C的对边分别为a、b、c, .
.
(1)求B;
(2)若 ,求C.
,求C.