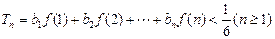（本题满分16分，第（1）小题6分，第（2）小题10分）
某团体计划于2011年年初划拨一笔款项用于设立一项基金，这笔基金由投资公司运作，每年可有3％的受益．
（1）该笔资金中的A（万元）要作为保障资金，每年年末将本金A及A的当年受益一并作为来年的投资继续运作，直到2020年年末达到250（万元），求A的值；
（2）该笔资金中的B（万元）作为奖励资金，每年年末要从本金B及B的当年受益中支取250（万元），余额来年继续运作，并计划在2020年年末支取后该部分资金余额为0，求B的值．（A和B的结果以万元为单位，精确到万元）
己知数列
满足：
，
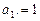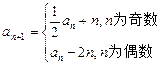
(1) 求a2，a3；
(2) 设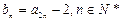
，求证
是等比数列，并求其通项公式；
(3) 在(2)条件下，求数列前100项中的所有偶数项的和S。
已知矩形ABCD，AD=2AB=2，点E是AD的中点，将△DEC
沿CE折起到△D’EC的位置，使二面角D'-EC -B是直二面角。
(Ⅰ) 证明：BE⊥CD’；
(Ⅱ) 求二面角D'-BC -E的余弦值，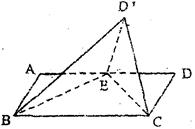
甲、乙、丙三人进行象棋比赛，每两人比赛一场，共赛三场．每场比赛胜者得3
分，负者得0分，没有平局，在每一场比赛中，甲胜乙的概率为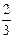
，甲胜丙的概率为
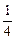，乙胜丙的概率为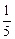
(1)求甲获第一名且丙获第二名的概率：
(2)设在该次比赛中，甲得分为ξ，求ξ的分布列和数学期望。
已知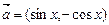
，
，函数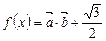
(1)求f(x)的最小正周期；
(2)当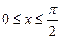
时，求函数f(x)的值域．
（本小题满分14分）
已知数列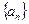
中，a1=3，a2=5，其前n项和Sn满足
令
(Ⅰ)求数列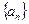的通项公式：
(Ⅱ)若
，求证：