(本小题满分14分)已知 抛物线
抛物线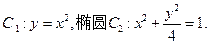
(1)设 是C1的任意两条互相垂直的切线,并设
是C1的任意两条互相垂直的切线,并设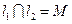 ,证明
,证明 :点M的纵坐标为定值;
:点M的纵坐标为定值;
(2)在C1上是否存在点P,使得C1在点P处切线与C2相交于两点A、B,且AB的中垂线恰为C1的切线?若存在,求出点P的坐标;若不存在,说明理由。
已知函数 函数
函数
 有相同极值点.
有相同极值点.
(1)求函数 的最大值;
的最大值;
(2)求实数 的值;
的值;
(3)若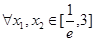 ,不等式
,不等式 恒成立,求实数
恒成立,求实数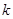 的取值范围.
的取值范围.
定义在 上的奇函数
上的奇函数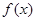 有最小正周期4,且
有最小正周期4,且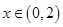 时,
时,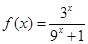 .
.
(1)求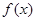 在
在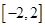 上的解析式;
上的解析式;
(2)判断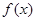 在
在 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当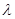 为何值时,关于方程
为何值时,关于方程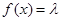 在
在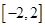 上有实数解?
上有实数解?
已知向量 ,
,
 ,函数
,函数 的图象与直线
的图象与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 .
.
(1)求函数 在
在 上的单调递增区间;
上的单调递增区间;
(2)将函数 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象.若
的图象.若 在
在 上至少含有
上至少含有 个零点,求
个零点,求 的最小值.
的最小值.
已知命题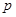 :函数
:函数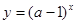 在
在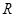 上单调递增;命题
上单调递增;命题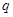 :不等式
:不等式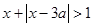 的解集为
的解集为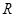 ,若
,若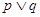 为真,
为真,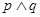 为假,求实数
为假,求实数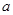 的取值范围.
的取值范围.
已知由不等式组 确定的平面区域
确定的平面区域 的面积为
的面积为 ,定点
,定点 的坐标为
的坐标为 ,若
,若 ,
, 为坐标原点,则
为坐标原点,则 的最小值是()
的最小值是()
A. |
B. |
C. |
D. |