(本小题满分14分)
已知 函数,其中
函数,其中 ,其中
,其中 。
。
(I)求函数 的零点;
的零点;
(II)讨论 在区间
在区间 上的单调性;
上的单调性;
(III)在区间 上,
上, 是否存在最小值?若存在,求出最小值;若不存在,请说明理由。
是否存在最小值?若存在,求出最小值;若不存在,请说明理由。
(本小题满分12分)
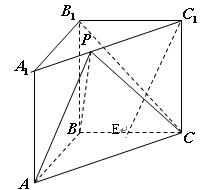
如图,在直三棱柱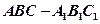 中,
中, ,
, 为
为 的中点,且
的中点,且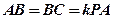 ,
,
(1)当 时,求证:
时,求证: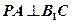 ;
;
(2)若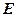 为
为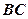 中点,当
中点,当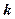 为何值时,异面直线
为何值时,异面直线
与 所成的角的正弦值为
所成的角的正弦值为 。
。
(本小题满分12分)
在一个盒子中放有标号分别为1、2、3的三张卡片,现从这个盒子中有放回地先后抽取两张卡片,并记它们的标号分别为 ,设
,设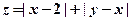 ,
,
(1)求事件“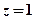 ”发生的概
”发生的概 率;
率;
(2)求 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率。
取得最大值”的概率。
(本小题满分12分)
已知函数 。
。
(1)若方程 在
在 上有解,求
上有解,求 的
的 取值范围;
取值范围;
(2)在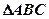 中,
中,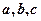 分别是
分别是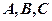 所对的边,当(1)中的
所对的边,当(1)中的 取最大值且
取最大值且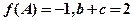 时,求
时,求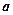 的最小值。
的最小值。
已知定义在正实数集上的函数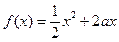 ,
, ,其中
,其中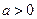 .设两曲线
.设两曲线 ,
, 有公共点,且在该点处的
有公共点,且在该点处的 切线相同.
切线相同.
(1 )用
)用 表示
表示 ,并求
,并求 的最大值;(2)求证:
的最大值;(2)求证: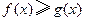 (
(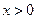 ).
).
(本小题满分12分)
已知直线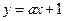 与双曲线
与双曲线 交于A、B两点,
交于A、B两点,
(1)若以AB线段为直径的圆过坐标原点,求实数a的值。
(2)是否存在这样的实数a,使A、B两点关于直线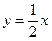 对称?说明理由.
对称?说明理由.