某单位决定投资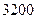 元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米造价
元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米造价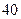 元,两侧墙砌砖,每米造价
元,两侧墙砌砖,每米造价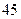 元,顶部每平方米造价
元,顶部每平方米造价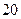 元,试问:(1)仓库面积
元,试问:(1)仓库面积 的最大允许值是多少?(2)为使
的最大允许值是多少?(2)为使 达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
(本小题满分10分)选修4-5:不等式选讲.
已知函数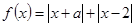 .
.
(1)当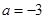 时,求不等式
时,求不等式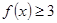 的解集;
的解集;
(2)若 的解集包含
的解集包含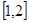 ,求
,求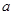 的取值范围.
的取值范围.
(本小题满分10分)选修4—4:坐标系与参数方程选讲.
已知直线经过点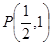 ,倾斜角
,倾斜角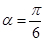 ,圆C的极坐标方程为
,圆C的极坐标方程为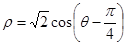
(1)写出直线的参数方程,并把圆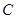 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)设与圆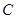 相交于两点
相交于两点 ,求点
,求点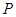 到
到 两点的距离之积.
两点的距离之积.
(本小题满分10分)选修4—1:几何证明选讲.
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O
交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
(1)求证: ;
;
(2)若 ,试求
,试求 的大小.
的大小.
(本小题满分12分)已知函数 ,
, .
.
(1)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)设函数 ,求函数
,求函数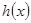 的单调区间;
的单调区间;
(3)若在 上存在一点
上存在一点 ,使得
,使得 成立,求
成立,求 的取值范围
的取值范围
(本小题满分12分)已知抛物线 ,直线
,直线 与抛物线交于
与抛物线交于 两点.
两点.
(1)若 轴与以
轴与以 为直径的圆相切,求该圆的方程;
为直径的圆相切,求该圆的方程;
(2)若直线与 轴负半轴相交,求
轴负半轴相交,求 面积的最大值
面积的最大值