设
,椭圆方程为
,抛物线方程为
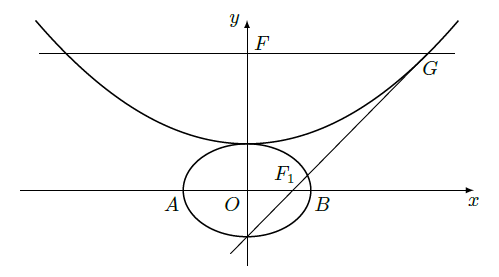
.如图所示,过点
作
轴的平行线,与抛物线在第一象限的交点为
,已知抛物线在点
的切线经过椭圆的右焦点
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
,使得
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
某地区注重生态环境建设,每年用于改造生态环境总费用为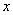 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少 亿元,至多
亿元,至多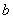 亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得每年改造生态环境总费用的22%。
亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得每年改造生态环境总费用的22%。
(1)若 ,
,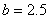 ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=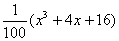 作为生态环境改造投资方案;
作为生态环境改造投资方案;
(2)若 、
、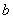 取正整数,并用函数模型y=
取正整数,并用函数模型y=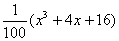 作为生态环境改造投资方案,请你求出
作为生态环境改造投资方案,请你求出 、
、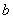 的取值.
的取值.
已知直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.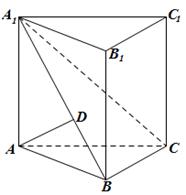
(1)求证:平面A1BC⊥平面ABB1A1;
(2)若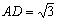 ,AB=BC=2,P为AC中点,求三棱锥
,AB=BC=2,P为AC中点,求三棱锥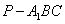 的体积。
的体积。
如图,在平面直角坐标系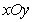 中,以
中,以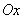 轴为始边,两个锐角
轴为始边,两个锐角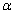 ,
, 的终边分别与单位圆相交于A,B 两点.
的终边分别与单位圆相交于A,B 两点.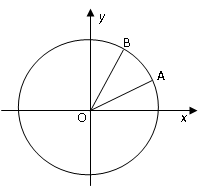
(Ⅰ)若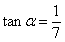 ,
,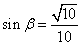 ,求
,求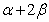 的值;
的值;
(Ⅱ)若角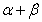 的终边与单位圆交于
的终边与单位圆交于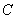 点,设角
点,设角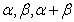 的正弦线分别为
的正弦线分别为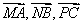 ,试问:以
,试问:以 作为三边的长能否构成一个三角形?若能,请加以证明;若不能,请说明理由.
作为三边的长能否构成一个三角形?若能,请加以证明;若不能,请说明理由.
已知向量
(Ⅰ)用含x的式子表示 及
及 ;
;
(Ⅱ)求函数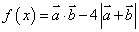 的值域;
的值域;
(Ⅲ)设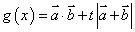 ,若关于x的方程
,若关于x的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数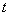 的取值范围.
的取值范围.
已知函数 ,且函数
,且函数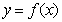 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为 .
.
(Ⅰ)求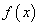 的对称中心;
的对称中心;
(Ⅱ)当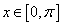 时,求
时,求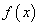 的单调增区间.
的单调增区间.