如图,在平面直角坐标系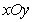 中,以
中,以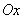 轴为始边,两个锐角
轴为始边,两个锐角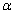 ,
, 的终边分别与单位圆相交于A,B 两点.
的终边分别与单位圆相交于A,B 两点.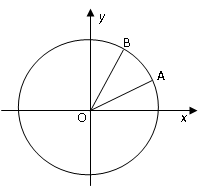
(Ⅰ)若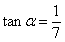 ,
,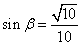 ,求
,求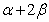 的值;
的值;
(Ⅱ)若角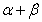 的终边与单位圆交于
的终边与单位圆交于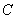 点,设角
点,设角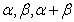 的正弦线分别为
的正弦线分别为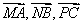 ,试问:以
,试问:以 作为三边的长能否构成一个三角形?若能,请加以证明;若不能,请说明理由.
作为三边的长能否构成一个三角形?若能,请加以证明;若不能,请说明理由.
如图,长方体 中,
中, ,点
,点 为
为 的中点.
的中点.
(1)求证:直线 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求 与平面
与平面 所成的角大小.
所成的角大小.
设全集为 ,集合
,集合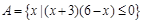 ,
,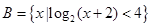 .
.
(1)求如图阴影部分表示的集合;
(2)已知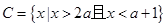 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
已知直线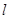 经过直线
经过直线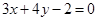 与直线
与直线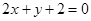 的交点
的交点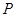 ,且垂直于直线
,且垂直于直线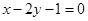 .
.
(1)求直线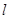 的方程;
的方程;
(2)求直线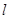 关于原点
关于原点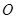 对称的直线方程.
对称的直线方程.
如果函数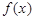 满足在集合
满足在集合 上的值域仍是集合
上的值域仍是集合 ,则把函数
,则把函数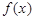 称为N函数.
称为N函数.
例如: 就是N函数.
就是N函数.
(Ⅰ)判断下列函数:①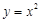 ,②
,②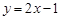 ,③
,③ 中,哪些是N函数?(只需写出判断结果);
中,哪些是N函数?(只需写出判断结果);
(Ⅱ)判断函数 是否为N函数,并证明你的结论;
是否为N函数,并证明你的结论;
(Ⅲ)证明:对于任意实数 ,函数
,函数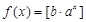 都不是N函数.
都不是N函数.
(注:“ ”表示不超过
”表示不超过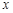 的最大整数)
的最大整数)
已知椭圆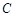 :
: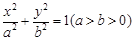 的离心率为
的离心率为 ,右焦点为
,右焦点为 ,右顶点
,右顶点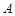 在圆
在圆 :
: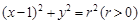 上.
上.
(Ⅰ)求椭圆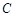 和圆
和圆 的方程;
的方程;
(Ⅱ)已知过点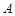 的直线
的直线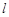 与椭圆
与椭圆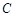 交于另一点
交于另一点 ,与圆
,与圆 交于另一点
交于另一点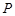 .请判断是否存在斜率不为0的直线
.请判断是否存在斜率不为0的直线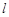 ,使点
,使点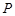 恰好为线段
恰好为线段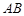 的中点,若存在,求出直线
的中点,若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.