某地区注重生态环境建设，每年用于改造生态环境总费用为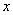
亿元，其中用于风景区改造为
亿元。该市决定建立生态环境改造投资方案，该方案要求同时具备下列三个条件：①每年用于风景区改造费用随每年改造生态环境总费用增加而增加；②每年改造生态环境总费用至少
亿元，至多
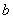亿元；③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%，但不得每年改造生态环境总费用的22%。
（1）若
，
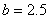，请你分析能否采用函数模型y＝
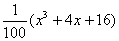作为生态环境改造投资方案；
（2）若、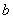取正整数，并用函数模型y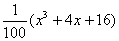＝作为生态环境改造投资方案，请你求出、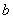的取值．
.
；
+
.
+(
+3sin
+(m2+2m-3)i,当m为何值时，（1）z∈R；（2）z是纯虚数；（3）z对应的点位于复平面第二象限；（4）z对应的点在直线x+y+3=0上.