(本题满分14分)
如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点.
(1)求证:BC与SA不可能垂直.
(2)设圆锥的高为4,异面直线AD与BC所成角的余弦值为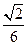 ,求圆锥的体积.
,求圆锥的体积.
设数列 为单调递增的等差数列
为单调递增的等差数列 且
且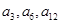 依次成等比数列.
依次成等比数列.
(Ⅰ)求数列 的通项公式
的通项公式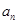 ;
;
(Ⅱ)若 求数列
求数列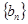 的前
的前 项和
项和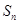 ;
;
(Ⅲ)若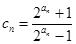 ,求证:
,求证: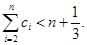
已知某公司生产某品牌服装的年固定成本为10万元,每生产一千件,需要另投入2.7万元.设该公司年内共生产该品牌服装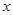 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为 万元,且
万元,且 .
.
(I)写出年利润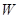 (万元)关于年产量
(万元)关于年产量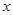 (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)年生产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
设函数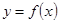 满足:对任意的实数
满足:对任意的实数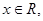 有
有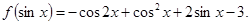
(Ⅰ)求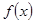 的解析式;
的解析式;
(Ⅱ)若方程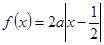 有解,求实数
有解,求实数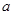 的取值范围.
的取值范围.
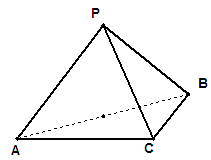
三棱锥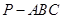 中,
中,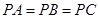 ,
,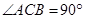 ,
,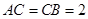 .
. 
(Ⅰ)求证:平面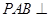 平面
平面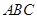 ;
;
(Ⅱ)若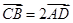 ,且异面直线
,且异面直线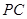 与
与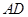 的夹角为
的夹角为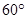 时,求二面角
时,求二面角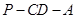 的余弦值.
的余弦值.
已知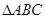 的面积
的面积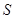 满足
满足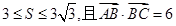 ,
,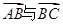 的夹角为
的夹角为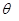 .
.
(Ⅰ)求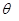 的取值范围;
的取值范围;
(Ⅱ)求函数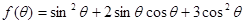 的最大值.
的最大值.