已知函数
（
）．
（1）当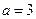
时，求函数
在
上的最大值和最小值；
（2）当函数在
单调时，求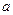
的取值范围；
（3）求函数既有极大值又有极小值的充要条件。
（本小题满分12分）
已知数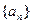列
和等比数列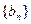
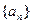，的前n项和为
，
，
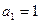且满足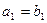
，
；
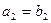（1）求数列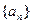的通项公式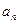
和等比数列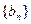的通项公式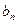
；
（2）求数列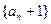
的前n项和
与等比数列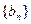的前n项和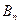
。
（本小题满分14分）
设函数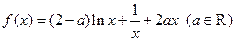
.
（Ⅰ）当
时，求
的极值；
（Ⅱ）当
时，求的单调区间；
（Ⅲ）若对任意
及
，恒有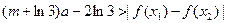
成立，求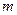
的取值范围.
（本小题满分14分）
数列{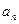
}、{
}的前n项和分别为
，
，且
=1（n∈N*）。
（1）证明数列{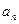}是等比数列；
（2）若数列{}满足：
，且
（n∈N*），求证：
(本题满分13分)
甲船在A处观察到乙船在它的北偏东
方向的B处，两船相距a 海里，乙船正向北行驶，若甲船速度是乙船速度的
倍，问甲船应取什么方向前进才能在最短时间内追上乙船，此时乙船行驶多少海里？
（本小题满分13分）
设函数
．
（Ⅰ）求
的最小正周期．
（Ⅱ）若函数
与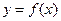
的图像关于直线
对称，求当
时的最大值．