已知圆C:x2+y2=r2(r>0)经过点(1,).
(1)求圆C的方程;
(2)是否存在经过点(-1,1)的直线l,它与圆C相交于A,B两个不同点,且满足=+(O为坐标原点)关系的点M也在圆C上?如果存在,求出直线l的方程;如果不存在,请说明理由.
已知甲、乙两煤矿每年的产量分别为200万吨和300万吨,需经过东车站和西车站两个车站运往外地,东车站每年最多能运280万吨煤,西车站每年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨.要使总运费最少,煤矿应怎样编制调运方案?
已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x-y-5=0.AC边上的高BH所在直线为x-2y-5=0.
求:(1)顶点C的坐标;
(2)直线BC的方程.
如图,直角三角形ABC的顶点A的坐标为(-2,0),直角顶点B的坐标为(0,-2),顶点C在x轴上.
(1)求BC边所在直线的方程.
(2)圆M是△ABC的外接圆,求圆M的方程.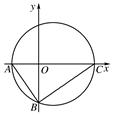
△ABC的两条高所在直线的方程为2x-3y+1=0和x+y=0,顶点A的坐标为(1,2),求BC边所在直线的方程.