如图,已知椭圆 的长轴
的长轴 ,离心率
,离心率 ,
, 为坐标原点,过
为坐标原点,过 的直线
的直线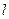 与
与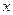 轴垂直,
轴垂直, 是椭圆上异于
是椭圆上异于 的任意一点,
的任意一点, ,
, 为垂足,延长
为垂足,延长 至
至 ,使得
,使得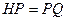 ,连接
,连接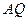 并延长交直线
并延长交直线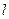 于
于 ,
, 为
为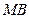 的中点
的中点
(1)求椭圆方程并证明 点在以
点在以 为直径的圆
为直径的圆 上
上
(2)试判断直线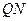 与圆
与圆 的位置关系
的位置关系
 |
已知

设两个非零向量a与b不共线, ⑴若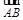 =a+b ,
=a+b , =2a+8b ,
=2a+8b ,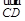 =3(a-b) ,
=3(a-b) ,
(1)求证:A、B、D三点共线;
(2)试确定实数k,使ka+b和a+kb共线.
(1)利用“五点法”画出函数 在长度为一个周期的闭区间的简图(要求列表描点)
在长度为一个周期的闭区间的简图(要求列表描点)
(本小题满分14分)已知二次函数 满足:①
满足:① 时有极值;②图象过点
时有极值;②图象过点 ,且在该点处的切线斜率为
,且在该点处的切线斜率为 .
.
(I)求f(x)的解析式;
(II)若曲线 上任意一点的切线的斜率恒大于
上任意一点的切线的斜率恒大于 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)当非零实数 满足什么条件时,函数
满足什么条件时,函数 的图象与坐标轴没有公共点?
的图象与坐标轴没有公共点?
(本小题满分12分)如图,椭圆 的顶点为
的顶点为 ,焦点为
,焦点为 ,
, .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ) 设n 为过原点的直线, 是与n垂直相交于P点,与椭圆相交于A, B两点的直线,
是与n垂直相交于P点,与椭圆相交于A, B两点的直线, .是否存在上述直线
.是否存在上述直线 使
使 成立?若存在,求出直线
成立?若存在,求出直线 的方程;并说出;若不存在,请说明理由.
的方程;并说出;若不存在,请说明理由.