如图所示，在一次消防演习中，消防员练习使用挂钩从高空沿滑杆由静止滑下，滑杆由AO、OB两段直杆通过光滑转轴连接地O处，可将消防员和挂钩均理想化为质点，且通过O点的瞬间没有机械能的损失。AO长为
=5m，OB长为
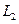=10m。两堵竖直墙的间距
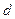=11m。滑杆A端用铰链固定在墙上，可自由转动。B端用铰链固定在另一侧墙上。为了安全，消防员到达对面墙的速度大小不能超过6m/s，挂钩与两段滑杆间动摩擦因数均为
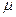=0.8。(
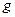=10m/s2，sin37°=0.6，cos37°=0.8)
（1）若测得消防员下滑时，OB段与水平方向间的夹角始终为37°，求消防员在两滑杆上运动时加速度的大小及方向；
（2）若B端在竖直墙上的位置可以改变，求滑杆端点A、B间的最大竖直距离。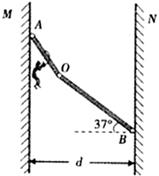
如图所示的电路，A、B之间电压保持不变，
，
，两个电压表的示数均为35V，如果将两个电压表的位置对调，则电压表V1的示数为30V，电压表V2的示数为40V，求两个电压表的电阻分别是多少？
如图所示，在匀强电场中，有A、B两点，它们间距为2cm，两点的连线与场强方向成60°角。将一个电量为−2×10−5C的电荷由A移到B，其电势能增加了0.1J。
则：（1）在此过程中，电场力对该电荷做了多少功？
（2）A．B两点的电势差UAB为多少？
（3）匀强电场的场强为多大？
如图所示，一个底面粗糙，质量为m的斜面体静止在水平地面上，斜面体斜面是光滑的，倾角为30°.现用一端固定的轻绳系一质量为m的小球，小球静止时轻绳与斜面的夹角是30°.
(1)求当斜面体静止时绳的拉力大小；
(2)若地面对斜面体的最大静摩擦力等于地面对斜面体支持力的k倍，为了使整个系统始终处于静止状态，k值必须满足什么条件？
为了最大限度地减少道路交通事故，全国开始了“集中整治酒后驾驶违法行为”专项行动．这是因为一般驾驶员酒后的反应时间比正常时慢了0.1～0.5 s，易发生交通事故．图示是《驾驶员守则》中的安全距离图示(如图所示)和部分安全距离表格.
| 车速 v(km/h) |
反应距离 s(m) |
刹车距离 x(m) |
停车距离 L(m) |
| 40 |
10 |
10 |
20 |
| 60 |
15 |
22.5 |
37.5 |
| 80 |
A |
40 |
60 |
请根据该图表回答下列问题(结果保留两位有效数字)：
(1)请根据表格中的数据计算驾驶员的反应时间．
(2)如果驾驶员的反应时间相同，请计算出表格中A的数据．
(3)假设在同样的路面上，刹车时加速度大小为6.2m/s，一名饮了少量酒的驾驶员驾车以72 km/h速度行驶，在距离一学校门前50 m处发现有一队学生在斑马线上横过马路，他的反应时间比正常时慢了0.2 s，会发生交通事故吗？
在十字路口，汽车以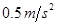
的加速度从停车线启动做匀加速直线运动，恰好有一辆自行车以
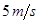的速度匀速驶过停车线与汽车同方向行驶，求：
（1）什么时候它们相距最远？最远距离是多少？
（2）在什么地方汽车追上自行车？追到时汽车的速度是多大？