已知函数 .
(Ⅰ)将函数 化简成 求 的周期;
(Ⅱ)求函数 ;在 上的最大值和最小值.
(本小题12分)(1)已知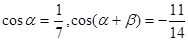 ,且
,且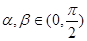 ,求
,求 的值;
的值;
(2)已知 为第二象限角,且
为第二象限角,且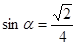 ,求
,求 的值.
的值.
(本小题12分)已知集合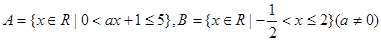 .
.
(1)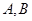 能否相等?若能,求出实数
能否相等?若能,求出实数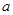 的值;若不能,试说明理由;
的值;若不能,试说明理由;
(2)若命题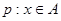 ,命题
,命题 ,且
,且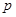 是
是 充分不必要条件,求实数
充分不必要条件,求实数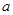 的取值范围.
的取值范围.
已知函数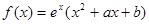 的图象在
的图象在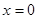 处的切线方程为
处的切线方程为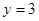 ,其中有e为自然对数的底数。
,其中有e为自然对数的底数。
(1)求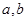 的值;
的值;
(2)当 时,证明
时,证明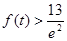 ;
;
(3)对于定义域为D的函数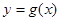 若存在区间
若存在区间 时,使得
时,使得 时,
时,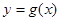 的值域是
的值域是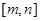 。则称
。则称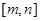 是该函数
是该函数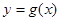 的“保值区间”。设
的“保值区间”。设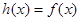 +
+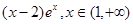 ,问函数
,问函数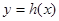 是否存在“保值区间”?若存在,求出一个“保值区间”,若不存在,说明理由。
是否存在“保值区间”?若存在,求出一个“保值区间”,若不存在,说明理由。
已知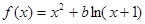 ,其中
,其中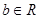 .
.
(1)若对 定义域内的任意x,都有
定义域内的任意x,都有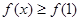 ,求b的值;
,求b的值;
(2)若函数 在其定义域内是单调函数,求b的取值范围;
在其定义域内是单调函数,求b的取值范围;
(3)若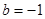 ,证明:对任意的正整数n,不等式
,证明:对任意的正整数n,不等式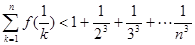 都成立。
都成立。
在锐角△ABC中,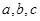 分别是角A,B,C的对边,
分别是角A,B,C的对边,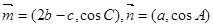 ,且
,且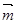 ∥
∥ 。
。
(1)求角A的大小;
(2)求函数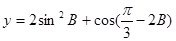 的值域。
的值域。