计算:(1) 
(2)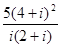
实数m取什么值时,复数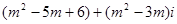 是
是
(1)实数;(2)虚数;(3)纯虚数。
设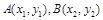 是椭圆
是椭圆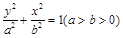 上的两点,已知向量
上的两点,已知向量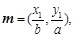
 ,若
,若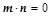 且椭圆的离心率
且椭圆的离心率 ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.
(1)求椭圆的方程;
(2)试问△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
设圆C与两圆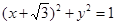 ,
, 中的一个内切,另一个外切.
中的一个内切,另一个外切.
(1)求C的圆心轨迹L的方程;
(2)设直线l是圆O: 在P(x0,y0)(x0y0 ≠ 0)处的切线,且P在圆上,l与轨迹L相交不同的A,B两点,证明:
在P(x0,y0)(x0y0 ≠ 0)处的切线,且P在圆上,l与轨迹L相交不同的A,B两点,证明: .
.
某商店试销某种商品,获得如下数据:
| 日销售量(件) |
0 |
1 |
2 |
3 |
| 概率 |
0.05 |
0.25 |
0.45 |
0.25 |
试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货再补充3件,否则不进货。
(Ⅰ)求当天商品不进货的概率;
(Ⅱ)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望。