如图, ,
, ,
, ,
, 为空间四点,且
为空间四点,且
 ,
,



 .等边三角形
.等边三角形 以
以 为轴转动.
为轴转动.
(Ⅰ)当平面
 平面
平面 时,求
时,求 ;
;
(Ⅱ)当△ 转动时,是否总有
转动时,是否总有


 ?证明你的结论.
?证明你的结论.
已知函数f(x)=x2-(a+2)x+alnx(a∈R)。
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若a=4,y=f(x)的图像与直线y=m有三个交点,求m的取值范围。
已知数列{an}(n为正整数)是首项为a1,公比为q的等比数列.
(1)求和: ( i )a1C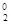 -a2C
-a2C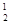 +a3C
+a3C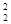 , ( ii )a1C
, ( ii )a1C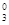 -a2C
-a2C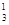 +a3C
+a3C -a4C
-a4C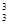 ;
;
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在1次游戏中,
(i)摸出3个白球的概率;(ii)获奖的概率;
(Ⅱ)求在2次游戏中获奖次数 的分布列及数学期望
的分布列及数学期望 .
.
为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
| 是否需要志愿性别 |
男 |
女 |
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人,需要志愿帮助的老年人的比例?说明理由
附:
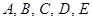 五人站成一排.求下列问题的排法总数;
五人站成一排.求下列问题的排法总数;
(1) 不站在排头也不站在排尾;(2)
不站在排头也不站在排尾;(2)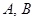 两人都不站在两端;
两人都不站在两端;
(3) 不站在排头,
不站在排头, 不站在排尾;(4)
不站在排尾;(4) 两两不相邻.
两两不相邻.