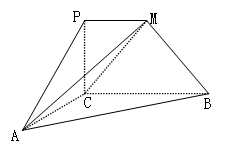
如图,在四棱锥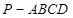 中,
中, ⊥底面
⊥底面 ,四边形
,四边形 是直角梯形,
是直角梯形, ⊥
⊥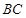 ,
, ∥
∥ ,
,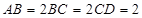 .
.

(Ⅰ)求证:平面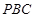 ⊥平面
⊥平面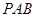 ;
;
(Ⅱ)若二面角 的余弦值为
的余弦值为 ,求
,求 .
.
已知函数f(x)=x2-(1+2a)x+aln x(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
已知
 ).
).
(1)若 时,求函数
时,求函数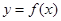 在点
在点 处的切线方程;
处的切线方程;
(2)若函数 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(3)令 是否存在实数
是否存在实数 ,当
,当 是自然对数的底)时,函数
是自然对数的底)时,函数 的最小值是
的最小值是 .若存在,求出
.若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知向量 ,
, ,且
,且 .
.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)设曲线 与直线
与直线 相交于不同的两点
相交于不同的两点 ,又点
,又点 ,当
,当 时,求实数
时,求实数 的取值范围.
的取值范围.
在数列 中,已知
中,已知 ,
,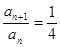 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 ,求
,求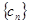 的前
的前 项和
项和 .
.
如图,四边形PCBM是直角梯形, ,
, ,
, ,
, .又
.又 ,
,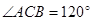 ,
,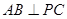 ,直线
,直线 与直线
与直线 所成的角为60°.
所成的角为60°.
(1)求证: ;
;
(2)求三棱锥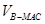 的体积.
的体积.