(本小题满分14分)
如图:在四棱锥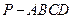 中,底面ABCD是菱形,
中,底面ABCD是菱形,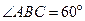 ,
,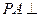 平面ABCD,点M,N分别为BC,PA的中
平面ABCD,点M,N分别为BC,PA的中 点,且
点,且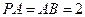
(I)证明: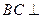 平面AMN;
平面AMN;
(II)求三棱锥N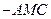 的体积;
的体积;
(III)在线段PD上是否存在一点E, 使得
使得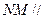 平面ACE;若存在,求出PE的长,若不存在,说明理由。
平面ACE;若存在,求出PE的长,若不存在,说明理由。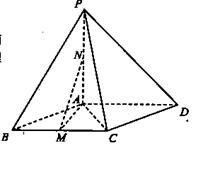
已知函数 .
(Ⅰ)设
,求
的单调期间;
(Ⅱ)设
在区间
中至少有一个极值点,求
的取值范围.
如图,由
到
的电路中有4个元件,分别标为
,电源能通过
的概率都是
,电源能通过
的概率是0.9,电源能否通过各元件相互独立。已知
中至少有一个能通过电流的概率为0.999.
(Ⅰ)求
;
(Ⅱ)求电流能在
与
之间通过的概率.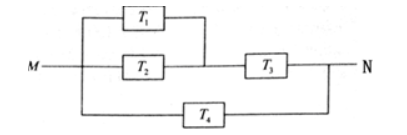
如图,直三棱柱 中, , , 为 的中点, 为 上的一点,
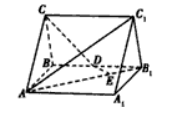
(Ⅰ)证明:
为异面直线
与
的公垂线;
(Ⅱ)设异面直线
与
的夹角为45°,求二面角
的大小
已知 是各项均为正数的等比数列,且 ,
(Ⅰ)求
的通项公式;
(Ⅱ)设
,求数列
的前
项和
。
中, 为边 上的一点, ,求 .