(本小题满分13分)
已知椭圆C的对称中心为原点O,焦点在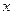 轴上,离心率为
轴上,离心率为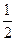 ,且点
,且点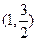 在该椭圆上.
在该椭圆上.
(I)求椭圆C的方程;
(II)过椭圆C的左焦点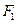 的直线
的直线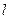 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若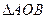 的面积为
的面积为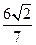 ,求圆心在原点O且与直线l相切的圆的方程.
,求圆心在原点O且与直线l相切的圆的方程.
12月30日晚上,高二年级举行2011年元旦“师生红歌会”,某班有4名老师和4名学生站成一排。
(1)全部站成一排,共有多少种不同的排法? (要求用数字作答)
(要求用数字作答)
(2)全部 站成一排,4名学生必须排在一起,共有多少种不同的排法?
站成一排,4名学生必须排在一起,共有多少种不同的排法? (要求用数字作答)
(要求用数字作答)
(3)全部站成一排,任两名学生都不能相邻,共有多少种不同的排法? (要求用数字作答)
(要求用数字作答)
已知双曲线与椭圆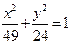 共焦点,且以
共焦点,且以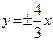 为渐近线,求双曲线方程
为渐近线,求双曲线方程
已知函数 .
.
(Ⅰ)若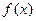 为
为 上的单调函数,试确
上的单调函数,试确 定实数
定实数 的取值范围;
的取值范围;
(Ⅱ)求函数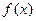 在定义域上的极值;
在定义域上的极值;
(Ⅲ)设 ,求证:
,求证: .
.
已知点A(2,0),
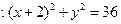 . P为
. P为 上
上 的动点,线段BP上的点M满足|MP|=|MA|.
的动点,线段BP上的点M满足|MP|=|MA|.
(Ⅰ)求点M的轨迹C的方程;
(Ⅱ)过点B(-2,0)的直线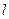 与轨迹C交于S、T两点,且
与轨迹C交于S、T两点,且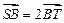 ,求直线
,求直线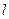 的方程.
的方程.
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为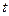 元(
元(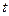 为常数,且
为常数,且 ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为 元(
元( ),根据市场调查,销售量
),根据市场调查,销售量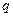 与
与 成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
(Ⅰ)求该工厂的每日利润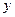 元与每公斤蘑菇
元与每公斤蘑菇 的出厂价
的出厂价 元的函数关系式;
元的函数关系式;
(Ⅱ)若 ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价 为多少元时,该工厂的利润
为多少元时,该工厂的利润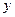 最大,并求最大值.
最大,并求最大值.