12月30日晚上，高二年级举行2011年元旦“师生红歌会”，某班有4名老师和4名学生站成一排。
（1）全部站成一排，共有多少种不同的排法？（要求用数字作答）
（2）全部
站成一排，4名学生必须排在一起，共有多少种不同的排法？（要求用数字作答）
（3）全部站成一排，任两名学生都不能相邻，共有多少种不同的排法？（要求用数字作答）
如右图，简单组合体ABCDPE，其底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD＝2EC.
(1)若N为线段PB的中点，求证：EN⊥平面PDB；
(2)若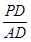
＝
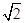，求平面PBE与平面ABCD所成的锐二面角的大小.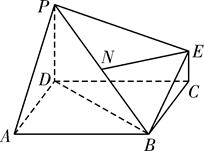
设△ABC的内角A，B，C所对的边长分别为a，b，c，m＝(cosA，cosC)，n＝(
c－2b，a)且m⊥n.
(1)求角A的大小；
(2)若角B＝
，BC边上的中线AM的长为
，求△ABC的面积.
已知函数f(x)=－x3＋3x2＋9x＋m
（I）求f(x)的单调递减区间；
（II）若f(x)在区间[－2，2]上的最大值为20，求它在该区间上的最小值．
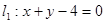直线
与直线
相交于点P，
求（1）过点P与直线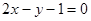
平行的直线方程；
（2）过点P与直线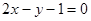垂直的直线方程。
在等差数列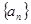
中，已知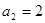
，
，
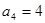（1）求数列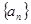的通项公式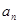
；
（2）设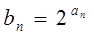
，求数列
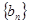前5项的和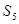
.