(本小题满分14分)
如图,在三棱柱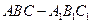 中,侧面
中,侧面 底面ABC,
底面ABC,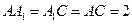 ,
, ,且
,且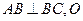 为AC中点.
为AC中点.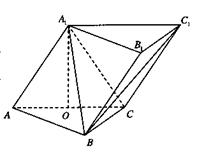
(I)证明: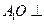 平面ABC;
平面ABC;
(II)求直线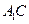 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(III)在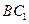 上是否存在一点E,使得
上是否存在一点E,使得 平面
平面 ,若不存在,说明理由;若存在,确定点E的位置.
,若不存在,说明理由;若存在,确定点E的位置.
(本小题满分12分)
在平面直角坐标系xOy中,曲线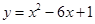 与坐标轴的交点都在圆C上
与坐标轴的交点都在圆C上
(1)求圆C的方程;
(2)若圆C与直线 交与A,B两点,且
交与A,B两点,且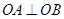 ,求a的值。
,求a的值。
(本小题满分12分)已知点P和点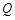 是曲线
是曲线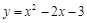 上的两点,且点
上的两点,且点 的横坐标是1,点
的横坐标是1,点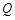
的横坐标是4,求:(1)割线的
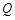 斜率;(2)点
斜率;(2)点 处的切线方程.
处的切线方程.
(本小题满分10分)求以椭圆 的焦点为顶点,以椭圆的顶点为焦点的双曲线的方程.
的焦点为顶点,以椭圆的顶点为焦点的双曲线的方程.
(满分12分)3.已知数列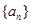 的前
的前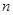 项和为
项和为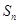 ,且有
,且有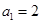 ,
,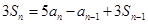

(1)求数列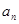 的通项公式;
的通项公式;
(2)若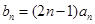 ,求数列
,求数列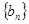 的前
的前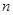 项的和
项的和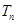 。山大附中
。山大附中
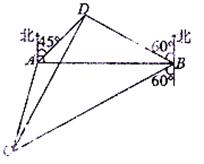
(满分12分)如图,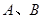 是海面上位于东西方向相距
是海面上位于东西方向相距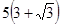 海里的两个观测点,现位于
海里的两个观测点,现位于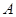 点北偏东
点北偏东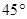 ,
,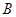 点北偏西
点北偏西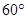 的
的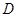 点有一艘轮船发出求救信号,位于
点有一艘轮船发出求救信号,位于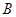 点南偏西
点南偏西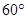 °且与
°且与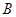 点相距
点相距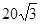 海里的
海里的 点的救援船立即即前往营救,其航行速度为
点的救援船立即即前往营救,其航行速度为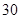 海里/小时,该救援船到达
海里/小时,该救援船到达 点需要多长时间?
点需要多长时间?