（本小题满分12分）
已知
、
分别是直线
和
上的两个动点，线段
的长为
，
是的中点．
（1）求动点的轨迹
的方程；
（2）过点
作直线
（与
轴不垂直）与轨迹交于
两点，与
轴交于点
．若
，
，证明：
为定值．
在扇形OAmB中，
,C为的 中点（如图）
（1）在上任取一点M，求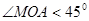
的概率；
（2）在OC上任取点N，过N作
,交于E,F，求EF<OA的概率（精确到0.01）
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量
(吨)与相应的生产能耗
(吨标准煤)的几组对照数据：
|
 |
 |
 |
 |
|
 |
|
|
 |
(1)请根据上表提供的数据，求出关于的线性回归方程
；
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(1)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
某中学从参加高一年级上期期末考试的学生中抽出60名学生，将其成绩（均为整数）分成六段
，
…
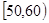后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：
（Ⅰ）估计这次考试的及格率（60分及以上为及格）；
(Ⅱ) 从成绩是70分以上（包括70分）的学生中选一人，求选到第一名学生的概率（第一名学生只一人）.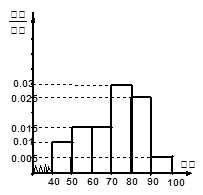 
已知函数
（1）
时，求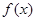
的单调区间；
（2）设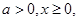
若
恒成立，求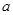
的取值范围.
如图，已知圆C：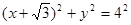
，定点A（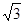
，0），M为圆C上一动点，点N在AM上，点P在 CM上，且满足
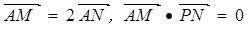，点P的轨迹为曲线E，
（1）求曲线E 的方程；
（2）当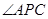
为钝角，求点P的横坐标的取值范围。