(本小题满分14分) 设函数
设函数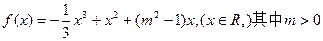 。
。
(Ⅰ)当 曲线
曲线 处的切线斜率(Ⅱ)求函数的单调区间与极值;(Ⅲ)已知函数
处的切线斜率(Ⅱ)求函数的单调区间与极值;(Ⅲ)已知函数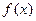 有三个互不相同的零点0,
有三个互不相同的零点0,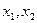 ,且
,且 。若对任意的
。若对任意的 ,
,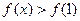 恒成立,求m的取值范围。
恒成立,求m的取值范围。
给定圆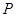 :
: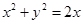 及抛物线
及抛物线 :
: ,过圆心
,过圆心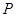 作直线
作直线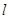 ,此直线与上述两曲线的四个交点,自上而下顺次记为
,此直线与上述两曲线的四个交点,自上而下顺次记为 ,如果线段
,如果线段 的长按此顺序构成一个等差数列,求直线
的长按此顺序构成一个等差数列,求直线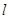 的方程.
的方程.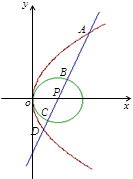
有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定.大桥上的车距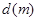 与车速
与车速 和车长
和车长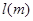 的关系满足:
的关系满足: (
(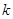 为正的常数),假定车身长为
为正的常数),假定车身长为 ,当车速为
,当车速为 时,车距为2.66个车身长.
时,车距为2.66个车身长.
写出车距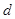 关于车速
关于车速 的函数关系式;
的函数关系式;
应规定怎样的车速,才能使大桥上每小时通过的车辆最多?
如图,四边形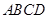 为矩形,平面
为矩形,平面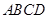 ⊥平面
⊥平面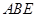 ,
,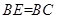 ,
,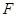 为
为 上的一点,且
上的一点,且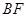 ⊥平面
⊥平面 .
. 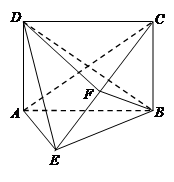
(1)求证: ⊥
⊥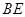 ;
;
(2)求证: ∥平面
∥平面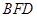 .
.
在锐角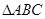 中,角
中,角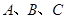 的对边分别为
的对边分别为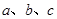 ,已知
,已知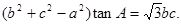
(1)求角 ;
;
(2)若 ,求
,求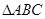 面积
面积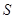 的最大值.
的最大值.
已知 是
是 的一个极值点.
的一个极值点.
(Ⅰ) 求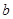 的值;
的值;
(Ⅱ) 求函数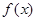 的单调递减区间;
的单调递减区间;
(Ⅲ)设 ,试问过点
,试问过点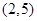 可作多少条直线与曲线
可作多少条直线与曲线 相切?请说明理由.
相切?请说明理由.