(本小题满分14分)某工厂三个车间共有工人1000名,各车间男、女工人数如下表:
| |
第一车间 |
第二车间 |
第三车间 |
| 女工 |
173 |
100 |
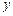 |
| 男工 |
177 |
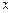 |
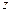 |
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求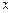 的值;
的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
(3)已知 ,求第三车间中女工比男工少的概率.
,求第三车间中女工比男工少的概率.
(本小题满分12分)
在 中,角
中,角 的对边分别为
的对边分别为 ,
, 是该三角形的面积,
是该三角形的面积,
(1)若 ,
, ,
, ,求角
,求角 的
的
度数;(2)若 ,
, ,
, ,求
,求 的值.
的值.
(本小题满分14分)
已知函数
(1)当a=1时,求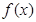 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;
(2)若在区间 上,函数
上,函数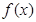 的图象恒在直线
的图象恒在直线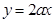 下方,求a的取值范围。
下方,求a的取值范围。
(本小题满分14分)
已知函数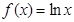 的图象是曲线C,点
的图象是曲线C,点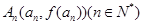 是曲线C上的一系列点,
是曲线C上的一系列点,
曲线C在点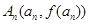 处的切线与y轴交于点
处的切线与y轴交于点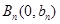 。若数列
。若数列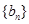 是公差为2的等差
是公差为2的等差
数列,且
(1)分别求出数列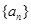 与数列
与数列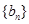 的通项公式;
的通项公式;
(2)设O为坐标原点, 表示
表示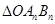 的面积,求数列
的面积,求数列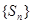 的前项n和
的前项n和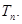
(本小题满分14分)
如图,设P是圆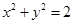 上的动点,点D是P在x轴上的投影。M为线段PD上一点,
上的动点,点D是P在x轴上的投影。M为线段PD上一点,
且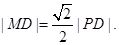
(1)当点P在圆上运动时,求点M的轨迹C的方程;
(2)已知点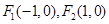 ,设点
,设点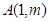
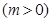 是轨迹C上的一点,求
是轨迹C上的一点,求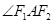 的
的
平分线 所在直线的方程。
所在直线的方程。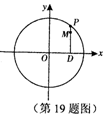
(本小题满分14分)
如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1。
将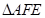 沿折起到
沿折起到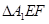 的位置,使平面
的位置,使平面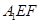 与平面BCFE垂直,连结A1B、A1P(如图2)。
与平面BCFE垂直,连结A1B、A1P(如图2)。
(1)求证:PF//平面A1EB;
(2)求证:平面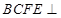 平面A1EB;
平面A1EB;
(3)求四棱锥A1—BPFE的体积。