(本小题满分16分)定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意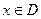 ,存在常数
,存在常数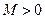 ,都有
,都有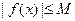 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中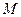 称为函数
称为函数 的上界.
的上界.
已知函数 ;
; .
.
(1)当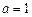 时,求函数
时,求函数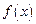 在
在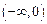 上的值域,并判断函数
上的值域,并判断函数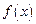 在
在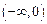 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数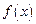 在
在 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 的取值范围;
的取值范围;
(3)若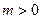 ,函数
,函数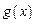 在
在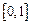 上的上界是
上的上界是 ,求
,求 的取值范围.
的取值范围.
(选修4—5:不等式选讲)设函数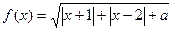 。
。
(1)当a=-5时,求函数 的定义域。
的定义域。
(2)若函数 的定义域为R,求实数a的取值范围。
的定义域为R,求实数a的取值范围。
(选修4—4:坐标系与参数方程)设直角坐标系的原点与极坐标系的极点重合,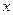 轴正半轴与极轴重合。已知圆C的极坐标方程:
轴正半轴与极轴重合。已知圆C的极坐标方程: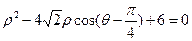
(I)将极坐标方程化为普通方程。
(II)若点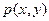 在圆C上,求
在圆C上,求 的取值范围。
的取值范围。
如图,BA是⊙O的直径,AD是⊙O切线,C、E分别
为半圆上不同的两点,BC交AD于D,BE交AD于F。
(I) 求证:BE·BF=BC·BD。
(II) 若⊙O的半径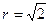 ,BC=1,求AD。
,BC=1,求AD。
设函数 ,
,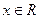 。
。
(1)求函数 的单调区间和极值。
的单调区间和极值。
(2)若关于 的方程
的方程 ="a" 有三个不同实根,求实数a的取值范围。
="a" 有三个不同实根,求实数a的取值范围。
(3)已知当 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
已知函数
 ,求
,求 的最大值和最小值。
的最大值和最小值。