(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分7分,第3小题满分6分.
已知数列 满足
满足 ,
, ,
, 是数列的前
是数列的前 项和,且
项和,且 (
(
 ).
).
(1)求实数 的值;
的值;
(2)求数 列
列 的通项公式;
的通项公式; (3)对于数列
(3)对于数列 ,若存在常数M,使
,若存在常数M,使 (
( ),且
),且 ,则M叫做数列
,则M叫做数列 的“上渐近值”.
的“上渐近值”.
设 (
( ),
), 为数列
为数列 的前
的前 项和,求数列
项和,求数列 的上渐近值.
的上渐近值.
某产品生产产家根据以往的生产销售经验得到下面有关销售的统计规律:每生产产品x(百台),其总成本为G(x)万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)满足
R(x)=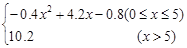
假定该产品销售平衡,那么根据上述统计规律:
(1)要使工厂有盈利,产量x应控制在什么范围?
(2)工厂生产多少台产品时盈利最大?并求此时每台产品的售价为多少?
如图,在平面直角坐标系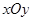 中,以
中,以 轴为始边作两个锐角
轴为始边作两个锐角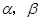 ,它们的终边分别交单位圆于
,它们的终边分别交单位圆于 两点.已知
两点.已知 两点的横坐标分别是
两点的横坐标分别是 ,
, .
.
(1)求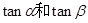 的值;
的值;
(2)求 的值.
的值.
设集合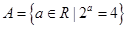 ,
,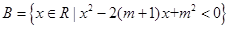 .
.
(1)若 ,求
,求 ;
;
(2)若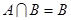 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知函数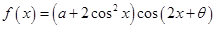 为奇函数,且
为奇函数,且 ,其中
,其中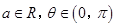 .
.
(1)求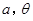 的值;
的值;
(2)若 ,求
,求 的值.
的值.
(本小题满分12分)已知函数
(1)用单调性的定义判断函数 在
在 上的单调性并加以证明;
上的单调性并加以证明;
(2)设 在
在 的最小值为
的最小值为 ,求
,求 的解析式.
的解析式.