某产品生产产家根据以往的生产销售经验得到下面有关销售的统计规律:每生产产品x(百台),其总成本为G(x)万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)满足
R(x)=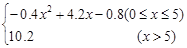
假定该产品销售平衡,那么根据上述统计规律:
(1)要使工厂有盈利,产量x应控制在什么范围?
(2)工厂生产多少台产品时盈利最大?并求此时每台产品的售价为多少?
已知函数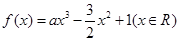 ,其中
,其中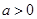 .
.
(1)若 ,求曲线
,求曲线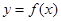 在点
在点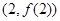 处的切线方程;
处的切线方程;
(2)求函数的极大值和极小值,若函数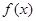 有三个零点,求
有三个零点,求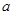 的取值范围.
的取值范围.
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
 |
 |
0 |
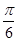 |
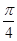 |
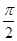 |
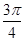 |
 |
0 |
1 |
 |
0 |
 |
0 |
(1)求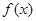 的解析式;
的解析式;
(2)若在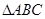 中,
中,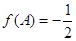 ,求
,求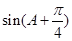 的值.
的值.
设函数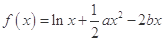 .
.
(1)当 ,
, 时,求函数
时,求函数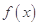 的最大值;
的最大值;
(2)令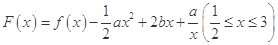 ,其图象上存在一点
,其图象上存在一点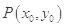 ,使此处切线的斜率
,使此处切线的斜率 ,求实数
,求实数 的取值范围;
的取值范围;
(3)当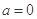 ,
, ,
,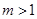 时,方程
时,方程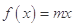 有唯一实数解,求
有唯一实数解,求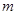 的值.
的值.
新晨投资公司拟投资开发某项新产品,市场评估能获得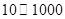 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金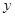 (单位:万元)随投资收益
(单位:万元)随投资收益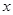 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于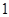 万元,同时不超过投资收益的
万元,同时不超过投资收益的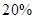 .
.
(1)设奖励方案的函数模型为 ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型 的基本要求.
的基本要求.
(2)下面是公司预设的两个奖励方案的函数模型:
①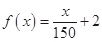 ;②
;②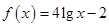
试分别分析这两个函数模型是否符合公司要求.
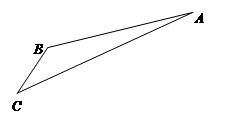
如图,游客在景点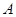 处下山至
处下山至 处有两条路径.一条是从
处有两条路径.一条是从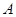 沿直道步行到
沿直道步行到 ,另一条是先从
,另一条是先从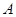 沿索道乘缆车到
沿索道乘缆车到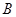 ,然后从
,然后从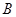 沿直道步行到
沿直道步行到 .现有甲、乙两位游客从
.现有甲、乙两位游客从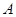 处下山,甲沿
处下山,甲沿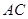 匀速步行,速度为
匀速步行,速度为 .在甲出发
.在甲出发 后,乙从
后,乙从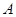 乘缆车到
乘缆车到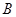 ,在
,在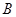 处停留
处停留 后,再从
后,再从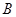 匀速步行到
匀速步行到 .假设缆车匀速直线运动的速度为
.假设缆车匀速直线运动的速度为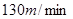 ,索道
,索道 长为
长为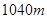 ,经测量
,经测量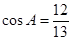 ,
, .
.
(1)求山路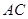 的长;
的长;
(2)假设乙先到,为使乙在 处等待甲的时间不超过
处等待甲的时间不超过 分钟,乙步行的速度应控制在什么范围内?
分钟,乙步行的速度应控制在什么范围内?